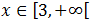Valor absoluto e inecuaciones
El valor absoluto de un número a, representado como |a|, es su valor numérico (con signo positivo).
Por ejemplo,
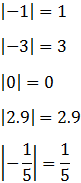
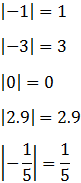
1. Función valor absoluto
Matemáticamente, el valor absoluto es una función (de una variable) de los reales en los reales:
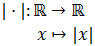
y se define como una función a trozos:
y se define como una función a trozos:
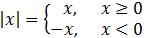 Esta función es continua en los reales y derivable en .
La gráfica de la función es:
Esta función es continua en los reales y derivable en .
La gráfica de la función es:
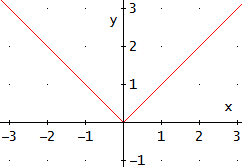 Notemos que en los reales negativos la gráfica es la de y = - x y en los positivos es la de y = x.
Notemos que en los reales negativos la gráfica es la de y = - x y en los positivos es la de y = x.
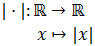
y se define como una función a trozos:
y se define como una función a trozos:
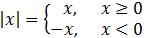 Esta función es continua en los reales y derivable en .
La gráfica de la función es:
Esta función es continua en los reales y derivable en .
La gráfica de la función es:
 Notemos que en los reales negativos la gráfica es la de y = - x y en los positivos es la de y = x.
Notemos que en los reales negativos la gráfica es la de y = - x y en los positivos es la de y = x.2. Propiedades del valor absoltuo
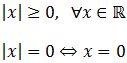
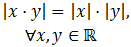
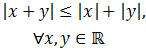
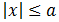
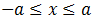
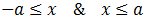
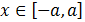
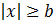
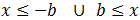
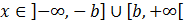
3. Inecuaciones con valor absoluto
Inecuación 1
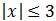 Escribimos la inecuación como
Escribimos la inecuación como
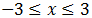 Por tanto, la solución es
Por tanto, la solución es
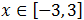 Inecuación 2
Inecuación 2
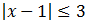 Podemos escribir la inecuación como
Podemos escribir la inecuación como
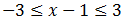 Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:Sumamos 1:
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:Sumamos 1:
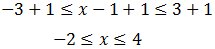 O bien, separar ambas inecuaciones y resolverlas por separado:
O bien, separar ambas inecuaciones y resolverlas por separado:
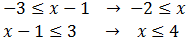 De ambas formas obtenemos la misma solución:
De ambas formas obtenemos la misma solución:
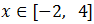 Inecuación 3
Inecuación 3
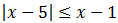 Escribimos la inecuación como:
Escribimos la inecuación como:
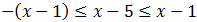 Vamos a trabajar primero con las dos inecuaciones al mismo tiempo:
Vamos a trabajar primero con las dos inecuaciones al mismo tiempo:
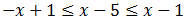 Sumamos 5:
Sumamos 5:
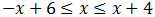 Sumamos x:
Sumamos x:
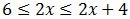 Ahora tenemos que separarlas para obtener la solución:
Por un lado:
Ahora tenemos que separarlas para obtener la solución:
Por un lado:
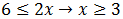 Por otro:
Por otro:
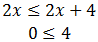 En esta segunda inecuación hemos obtenido una relación que siempre se cumple. Luego no nos aporta restricciones a la solución.Por tanto, la solución es
En esta segunda inecuación hemos obtenido una relación que siempre se cumple. Luego no nos aporta restricciones a la solución.Por tanto, la solución es
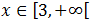
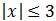 Escribimos la inecuación como
Escribimos la inecuación como
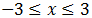 Por tanto, la solución es
Por tanto, la solución es
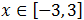 Inecuación 2
Inecuación 2
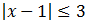 Podemos escribir la inecuación como
Podemos escribir la inecuación como
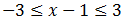 Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:Sumamos 1:
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:Sumamos 1:
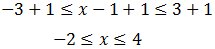 O bien, separar ambas inecuaciones y resolverlas por separado:
O bien, separar ambas inecuaciones y resolverlas por separado:
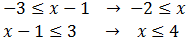 De ambas formas obtenemos la misma solución:
De ambas formas obtenemos la misma solución:
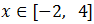 Inecuación 3
Inecuación 3
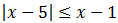 Escribimos la inecuación como:
Escribimos la inecuación como:
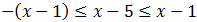 Vamos a trabajar primero con las dos inecuaciones al mismo tiempo:
Vamos a trabajar primero con las dos inecuaciones al mismo tiempo:
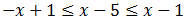 Sumamos 5:
Sumamos 5:
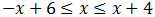 Sumamos x:
Sumamos x:
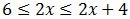 Ahora tenemos que separarlas para obtener la solución:
Por un lado:
Ahora tenemos que separarlas para obtener la solución:
Por un lado:
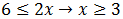 Por otro:
Por otro:
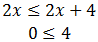 En esta segunda inecuación hemos obtenido una relación que siempre se cumple. Luego no nos aporta restricciones a la solución.Por tanto, la solución es
En esta segunda inecuación hemos obtenido una relación que siempre se cumple. Luego no nos aporta restricciones a la solución.Por tanto, la solución es