Tangenti a una circonferenza per un punto
Quante sono le tangenti alla circonferenza passanti per un punto?
Si possono presentare tre casi, a seconda della posizione del punto:
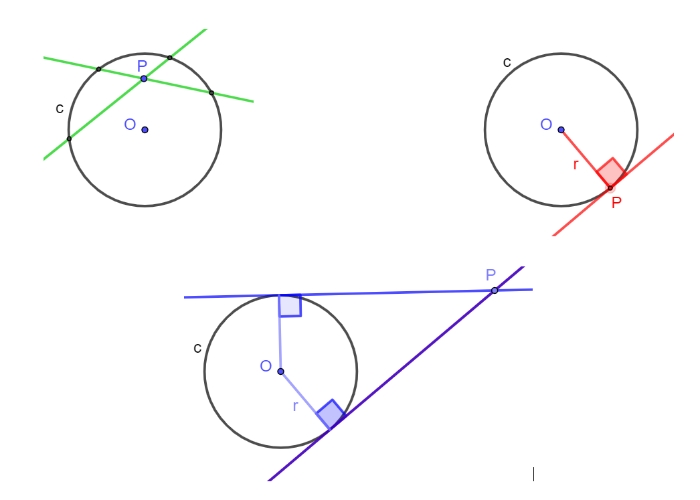
- Se il punto è interno alla circonferenza, non esistono tangenti alla circonferenza passanti per P. Infatti, ogni semiretta con origine in P, incontra la circonferenza in un punto, per l'assioma relativo alla circonferenza, in quanto congiunge P con un punto (infiniti, veramente) esterno alla circonferenza. Pertanto, ogni retta passante per P incontra la circonferenza in 2 punti e quindi, è secante e non tangente.
- Se il punto P appartiene alla circonferenza, esiste una e una sola tangente alla circonferenza passante per P: la retta che ha distanza dal centro congruente al raggio, cioè la perpendicolare al raggio OP in P (quindi, l'esistenza e unicità della tangente deriva dall'esistenza e unicità della perpendicolare).
- Se il punto è esterno alla circonferenza, esistono due tangenti alla circonferenza passanti per P.
Teorema: segmenti di tangente
Condotte per un punto P esterno a una circonferenza le due tangenti, si ha:
- i segmenti di tangente sono congruenti;
- la semiretta di origine P che passa per il centro della circonferenza è bisettrice dell'angolo formato dalle tangenti
- la semiretta di origine P che passa per il centro della circonferenza è bisettrice dell'angolo formato dai raggi passanti per i punti di tangenza.
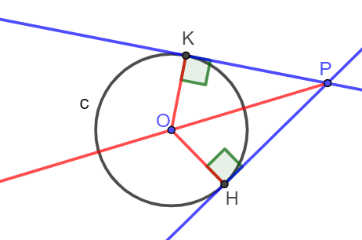
Dimostrazione
Ipotesi: PH e PK sono tangenti
Tesi:
PH PK
gli angoli HPO e KPO sono congruenti
gli angoli HOP e KOP sono congruenti
Dimostrazione
I due triangoli HOP e KOP sono rettangoli perchè la tangente è perpendicolare al raggio nel punto di tangenza e hanno l'ipotenusa OP in comune e i cateti OH e OK congruenti perchè sono raggi della stessa circonferenza. Pertanto, i due triangoli HOP e KOP sono congruenti per il criterio di congruenza dei triangoli rettangoli.
Di conseguenza, PH PK, HOP KOP e OPH OPK perchè sono elementi corrispondenti in triangoli congruenti.