Pythagorean Theorem
Teacher Instructions
Discovering the Pythagorean Theorem for Geometry Students (Grade 9-10)
This activity takes students through a discovery based learning experience about the Pythagorean Theorem. They will explore the relationship between the side lengths of perfect squares and how they form right triangles, if they do at all.
SCCCR G.GSRT.8* Solve right triangles in applied problems using trigonometric ratios and the
Pythagorean Theorem.
Objectives: Students will be able to:
Understand the properties of the Pythagorean Theorem (PT)
Use the PT to solve real world problems.
Materials: Geogebra activity, pencil, and paper
You should have discovered that the three triangles used to make a perfect right triangle are of side lengths 3, 4, and 5! Now, what does it mean that we are using squares? If the side lengths of each three squares are a, b, and c, respectively, how can we show the area of each square using mathematics?
The rule you have come up with should look something like this:
This is a discovery that was made over 2,000 years ago by Pythagoras! He found that when a triangle has a right angle and squares are made on each of the three sides, then the biggest square has the exact same area as the sum of the two smaller squares! How neat! This rule is called the Pythagorean Theorem and is used to find the length of a side of a triangle given the measure of the other two sides.
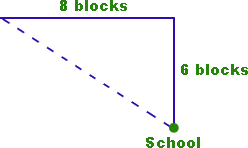
Peter leaves school and walks 6 blocks north, then 8 blocks west to get home. How many blocks would Peter walk if he went straight home from school?