べき級数でルジャンドル
ルジャンドルの多項式
1。べき級数で解く
このワークシートはMath by Codeの一部です。
前回まで、微分方程式の解法をさまざま見てきた。
今回は、べき級数を利用して、微分方程式の解法につなげてみよう。
<べき級数で微分方程式を解く>
べき級数と言えば、マクローリン級数(テーラー展開)が有名だ。
exp x= 1 + x + x^2/2! + x^3/3! +
cos x = 1 - x^2/2! + x^4/ 4! - + ....
sin x = x - x^3/3! + x^5/5! - + ....
これらは、級数展開が無限に続く表現になっている。
f(x)のテーラー級数展開Σ(a_m (x-b)m)がx=bの半径Rの近傍で収束するとき、f(x)はx=bで解析的だという。上記のようにb=0にした単純な形を特にマクローリン展開と呼ぶ。マクローリン展開が収束する
ときは、x=0で解析的という。
ほかにも、べき級数展開の公式がある。
また、等比級数展開
1/(1-x)=1+x+x2+x3+....の両辺をxで0からxまで積分すると
-lox(1-x)=x+1/2x2+1/3x3+..........
xに-xを代入すると,
log(1+x)=x-1/2x2+1/3x3-+.......
これから1/2(ln(1+x)-ln(1-x))=x+1/3x3+1/5x5+.....
微分方程式の解の関数もべき級数展開できたとすると
y=a_0+a_1x+a_2x^2+ a_3x^3+ ........... + a_kx^k+..... =Σ(a_m xm) [ m for 0 to ∞]
とおける。
y'= a_1 +2a_2x + 3a_3x^2 + .......... + ka_kx^(k-1) +......1 =Σ(m a_m xm-1) [ m for 1 to ∞]
y''= 2 a_2 + 3・2 a_3 x + ........ + k(k-1) a_k x^(k-2) + ......
=Σ(m(m-1) a_m xm-2) [ m for 2 to ∞]
となる。
微分方程式y''+p(x)y'+q(x)y-r(x)=0の係数p(x),q(x),r(x)がx=aで解析的なら、解yもx=aで解析的だ。
定数や多項式はべき級数の形にかけて、その係数は0だから、収束するので解析的。
たとえば、微分方程式 y' = 2xy
係数-2x=0+(-2)x+0x^2+0....でx=0において解析的。
関数を2x以外をすべてべき級数に置き換えてみよう。
left= a1 +2a2x + 3a3x^2 + .......... + kakx^(k-1) +......
right = 2x(a0+a1x+a2x^2+ a3x^3+ ........... + akx^k+.....)
左右の辺の同じ次数の項目の係数が等しいから、
a1=0 ,2a_2=2a_0 , 3a_3=2a_1, 4a_4=2a_2, 5a_5= 2a_3, 6a_6=2a_4
a_odd=0
a_even , a_0=Cとおくと、a_2k=C{1, 1,1/2, 1/3!, 1/4!,....}
これから、y=C(1+ 1x^2+1/2 x^4+ 1/3! x^6 + 1/4! x^8+....} =C exp(x^2) が解となる。
(例)
微分方程式y''=-y
係数-1=-1+0x + 0x^2+.......でx=0において解析的。
left= 2 a2+ 3*2 a3 x + 4*3 a4x^2 +5*4x^3........ + k(k-1) ak x^(k-2) + ......
right = -a0 -a1x - a2x^2 -a3x^3+ ........... + akx^k+..... 係数比較
2*1a_2=-a_0, 3*2a_3=-a_1, 4*3a_4= -a_2, 5*4a_5=-a_3, 6*5a_6=-a_4
a_0=A, a_1=Bとおくと
a_even=A{1,-1/2!, 1/4!, -1/6!, .....} , a_odd=B{1,-1/3!, 1/5!, -1/7!,......}
これから、y=A cos x + B sin x
2。ルジャンドルの微分方程式
<微分方程式>
nが実数のときLの解yはxの関数とする。
ルジャンドルの微分方程式L=(1-x2)y''-2xy' +n(n+1)y=0 の解を考える。
y''-2x/(1-x2)y' +n(n+1)/(1-x2)y=0係数p(x)=-2x/(1-x2)=-2x(1+x2+x4+.....),q(x)=n(n+1)/(1-x2)=n(n+1)(1+x2+x4+....)は解析的。
だから、x=0は正則点だ。
正則点の付近ではL=0は、y=Σ(a_m xm) [ m for 0 to ∞]べき級数解をもつ。
式を簡単にみせるために n(n+1)=kとおく。
(1-x2)y''-2xy' +n(n+1)y
=y''- x2y''-2xy' +ky=0
y=Σ(a_m xm) [ m for 0 to ∞]とするとき、y’’,y'もべき級数にして4項に代入して、xmの係数を取り出そう。
+ky==>+k am
-2xy'=-2xΣ(m a_m xm-1)から==> -2m am
- x2y''==> -m(m-1) am
y''=Σ(m(m-1) am xm-2)からmにm+2を代入して==>(m+2)(m+1) am+2
xmの係数は、(m+2)(m+1) am+2 -m(m-1) am-2m am+k am=0
まとめてみよう。
(m+2)(m+1) am+2+ [-m(m-1) +(k-2m)]am
=(m+2)(m+1) am+2+ [n2+n-m-m2]am
=(m+2)(m+1)am+2 + (n-m)(n+m+1) am=0
だから、
(いろんなnに対してmを動かす漸化式)。
すると、
,
,,,,,,,,,,,,,,,,,,,,,
<ルジャンドル関数>
以上のようにして、
いろんな実数nに対して整数mを動かす漸化式
から、
mが偶数か奇数かで2系列の数列ができるので、
解はy=a_0 y0(x) + a_1 y1(x)とかける。
y(x)=a_0(1+a_2/a_0x^2+a_4/a_0x^4+........) + a_1(x+ a_3/a_1 x^3 + a_5/a_1 x^5 +........)
y0(x),y1(x)はそれぞれ、ルジャンドル関数という。
y0(x)= [s for 0 to ∞]
y1(x)= [s for 0 to ∞]
(例)
n=0のとき
y1(x)=
=
n=1のとき
y0(x)=
=
<ルジャンドル多項式>
解y=Σ(a_m xm) [ m for 0 to ∞]の
mは非負の整数を動く。
nも非負の整数を動くと限定してみよう。
漸化式に(n-m)の因数があるから、m番目が変数nになった時点でそのあとはゼロ倍になる。
つまり、添え字mを動かしても最高でもaの添え字はnで止まる。つまり解yはn次多項式になるね。
解yはn次多項式で、Pn(x)とかき、これをルジャンドル多項式という。
逆にanを仮定してan-2, an_4,.....とカウントダウンすることもできるはず。
最高次のanをたとえば、
を仮定してみよう。つまり,自然数分の奇数をn個かけた値だ。
・次はカウントダウンの規則性を探ってみよう。
漸化式 の添え字mにnからのカウントダウンを入れよう。
だから、
最高次の2つ下の係数は、
だから、
最高次の4つ下の係数は、
............
これから推理して、
これをn-2m=1か0になるまで、mを動かして
xの(n-2m)次の係数としてたし上げたn次多項式がルジャンドルの多項式Pn(x)になるね。
nが偶数ならば最低次数は0まで、nが奇数なら最低次数は1までとなる。
mの最大値はn/2の商の切り捨てだから、ガウス記号[n/2]かシーリング関数を使う。
Pn(x)=Σ(an-2m)[ m for 0 to [n/2]] となる。
・では、P0(x)からP5(x)まで求めてみよう。
最高次の係数a_nの値は だから、自然数分の奇数という分数の積だった。
n=0,1,2,3,4,5の順に
漸化式からカウントダウンを入れよう。
だから、
n=0のとき、解は0次式でP0(x)=1
n=1のとき、解は1次式でP1(x)=1x
n=2のとき、解は2次式で、a_n=3/2, a_n-2=3/2*[-2(2-1)/2(2*2-1)]=3/2*(-1/3)=-1/2から、P2(x)=3/2x2-1/2
n=3のとき、解は3次式で、a_n=5/2, a_n-2=5/2*[-3(3-1)/2(2*3-1)]=5/2*(-3/5)=-3/2から、P3(x)=5/2x3-3/2x
n=4のとき、解は4次式で、a_n=35/8, a_n-2=35/8*[-4(4-1)/2(2*4-1)]=35/8*(-6/7)=-15/4、
a_n-4=-15/4*[-(4-2)(4-3)/4(2*4-3)]=-15/4*(-1/10)=3/8から、P4(x)=35/8x4-15/4x2-3/8
n=5のとき、解は5次式で、a_n=63/8, a_n-2=63/8*[-5(5-1)/2(2*5-1)]=63/8*(-10/9)=-35/4、
a_n-4=-35/4*[-(5-2)(5-3)/4(2*5-3)]=-35/4*(-3/14)=15/8から、P4(x)=63/8x5-35/4x3+15/8x
3.実装
質問:ルジャンドル多項式を求めるコードはどうやって作りますか。
scipyモジュールにはlegendre多項式のn次式を求める関数legendre(n,x)があります。
sympyモジュールでは、latex形式で表示する宣言init_printing()と関数displayがあります。
楽すぎてつまらないですね。
苦労したければ、n次式として最高次の係数を自然数分の奇数の積を求め、
そこに次数を2ずつさげた係数の比をnにあわせて次数が正である限り計算する。
それをxにかけた式にして、latexにして表示する。
という3ステップを繰り返すことになるでしょう。
#[IN]Python===============
from scipy import *
from sympy import *
from sympy.abc import x
for i in range(10):
Legendre = legendre(i, x)
print(f"P{i}(x)=",end="")
init_printing()
display(Legendre)
#[OUT]==================

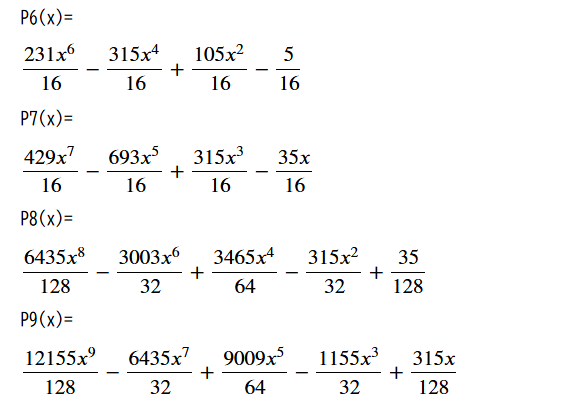
<ロドリグの公式>
ルジャンドルの多項式Pn(x)を求めるには、(n+1)Pn+1(x)=(2n+1)xPn(x)-nPn-1(x)
という漸化式を使う方法もありますが、
一気に求める公式、ロドリグの公式があります。
Pn(x)=
質問:ロドリグの公式をコードにするにはどうしたらよいですか。
lege=(x^2-1)^iのように多項式を定義して、
それを lege = diff(lege)をi回実行することで、i回微分すればよいね。
さらにそれを、2^i*factorial(i)で割りましょう。sympyにはfactorial関数があるので
そのまま使います。
ただ、結果の式がとても複雑になるので、
Legend=Legend.simplify()によって、式の単純化をしたものを表示します。
#[IN]Python=================================
from scipy import *
from sympy import *
from sympy.abc import x
print(f"P{0}(x)=",end="")
Lege=1
init_printing()
display(Lege)
for i in range(1,10):
lege=(x**2-1)**i
for j in range(1,i+1):
lege = diff(lege)
Legend= lege /( 2**i * factorial(i) )
Legend=Legend.simplify()
print(f"P{i}(x)=",end="")
init_printing()
display(Legend)
#[OUT]===============================
(省略)