L3.5 - Splitting Triangle Sides with Dilation, Part 1
Learning Intentions and Success Criteria:
- Justify that a segment dividing two sides of a triangle proportionally is parallel to the third side.
- Prove that a segment connecting the midpoints of two sides of a triangle is parallel to and half the length of the third side (orally and in writing).
- Explain why the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half the length of the third side.
5.1: Notice and Wonder: Midpoints
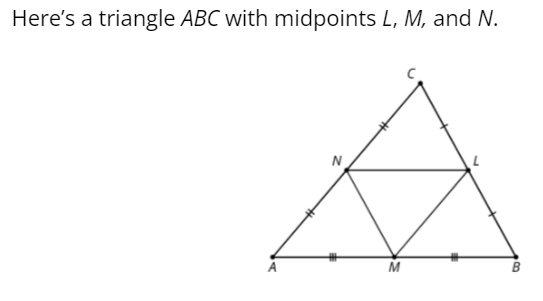
What do you notice? What do you wonder?
5.2: Dilation or Violation?
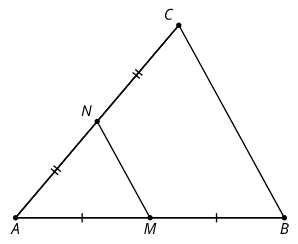
Here’s a triangle ABC. Points M and N are the midpoints of 2 sides. 1. Convince yourself triangle ABC is a dilation of triangle AMN. What is the center of the dilation? What is the scale factor?
2. Check the definition of dilation in your glossary. Does triangle ABC definitely fit the definition of dilation? 3. Prove that BC = 2MN.
5.3: A Little Bit Farther Now
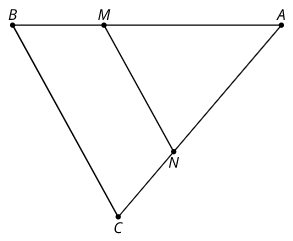
Here’s a triangle ABC. 1. M is ⅔ of the way from A to B. Dilate point B from point A using the fraction. Change B' to M. 2. N is ⅔ of the way from A to C. Dilate point C from point A using the fraction. Change C' to N. Make segment MN. 3. What can you say about segment MN compared to segment BC? Provide a reason or show work in the applet for each of your conjectures.

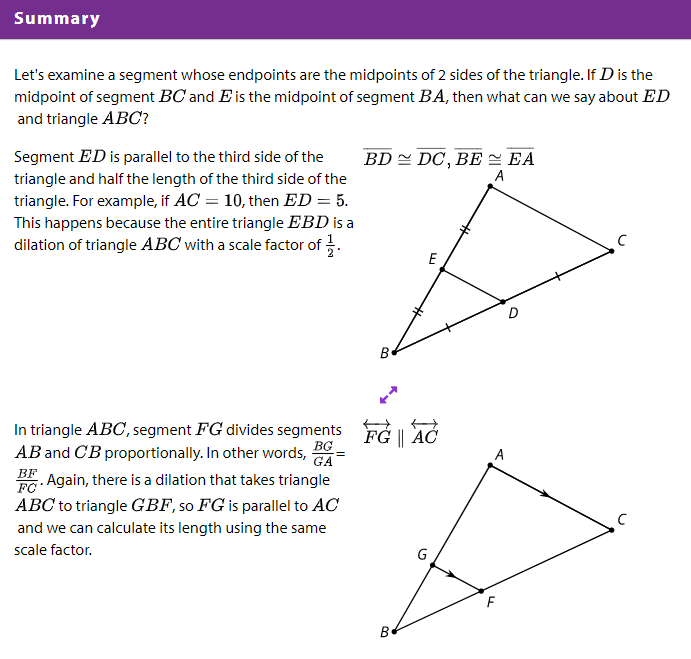
Learning Intentions and Success Criteria
- Justify that a segment dividing two sides of a triangle proportionally is parallel to the third side
- Prove that a segment connecting the midpoints of two sides of a triangle is parallel to and half the length of the third side (orally and in writing)
- Explain why the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half the length of the third side
Cool-Down: Missing Length
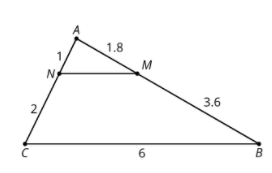
1. What must be true about segment MN?
2. Find the length of segment MN.

