Copia de Movimiento rectilíneo uniforme (MRU)
En esta página vamos a resolver problemas de movimiento rectilíneo uniforme (MRU), es decir, problemas de móviles que se mueven en línea recta y a velocidad constante.
La fórmula del MRU es
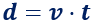 siendo
siendo
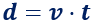 siendo
siendo
- d la distancia recorrida,
- v la velocidad del móvil
- t el tiempo que dura el movimiento
Problema 1
 ¿A qué velocidad debe circular un auto de carreras para recorrer 50km en un cuarto de hora?
Como la distancia es en kilómetros, vamos a escribir el tiempo en unidades de hora para tener la velocidad en km/h.
El tiempo que dura el movimiento es
¿A qué velocidad debe circular un auto de carreras para recorrer 50km en un cuarto de hora?
Como la distancia es en kilómetros, vamos a escribir el tiempo en unidades de hora para tener la velocidad en km/h.
El tiempo que dura el movimiento es
 La distancia recorrida por el móvil es
La distancia recorrida por el móvil es
 Por tanto, su velocidad debe ser
Por tanto, su velocidad debe ser
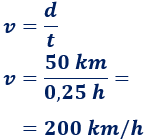
 ¿A qué velocidad debe circular un auto de carreras para recorrer 50km en un cuarto de hora?
Como la distancia es en kilómetros, vamos a escribir el tiempo en unidades de hora para tener la velocidad en km/h.
El tiempo que dura el movimiento es
¿A qué velocidad debe circular un auto de carreras para recorrer 50km en un cuarto de hora?
Como la distancia es en kilómetros, vamos a escribir el tiempo en unidades de hora para tener la velocidad en km/h.
El tiempo que dura el movimiento es
 La distancia recorrida por el móvil es
La distancia recorrida por el móvil es
 Por tanto, su velocidad debe ser
Por tanto, su velocidad debe ser
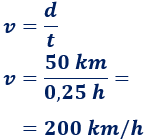
Problema 2: Una bicicleta circula en línea recta a una velocidad de 15km/h durante 45 minutos. ¿Qué distancia recorre?
La velocidad de la bicicleta es
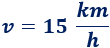 El tiempo que dura el movimiento es
El tiempo que dura el movimiento es
 Como las unidades de velocidad son kilómetros por hora y el tiempo está en minutos, tenemos que pasar el tiempo t de minutos a horas (dividiendo entre 60):
Como las unidades de velocidad son kilómetros por hora y el tiempo está en minutos, tenemos que pasar el tiempo t de minutos a horas (dividiendo entre 60):
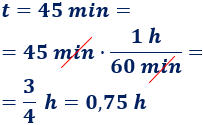 Calculamos la distancia que recorre la bicicleta:
Calculamos la distancia que recorre la bicicleta:

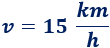 El tiempo que dura el movimiento es
El tiempo que dura el movimiento es
 Como las unidades de velocidad son kilómetros por hora y el tiempo está en minutos, tenemos que pasar el tiempo t de minutos a horas (dividiendo entre 60):
Como las unidades de velocidad son kilómetros por hora y el tiempo está en minutos, tenemos que pasar el tiempo t de minutos a horas (dividiendo entre 60):
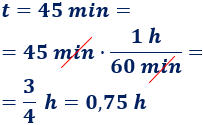 Calculamos la distancia que recorre la bicicleta:
Calculamos la distancia que recorre la bicicleta:

Más problemas resueltos:
- Problemas de movimiento rectilíneo uniforme (MRU)
- Integración por partes
- Ecuaciones exponenciales explicadas
- Problemas de mínimo común múltiplo y máximo común divisor
- Introducción a las progresiones: aritméticas y geométricas
- Ecuaciones de segundo grado paso a paso
- Problemas de sistemas de ecuaciones
- Problemas de ecuaciones
- Sistemas de ecuaciones (métodos)
- Ecuaciones de primer grado paso a paso
- Teorema de Pitágoras: problemas
- Potencias: propiedades y ejemplos
- Fracciones equivalentes y fracción irreductible
- Problemas y Ecuaciones .com