"Ikaw na ba si Mr. Right?": Activity on Triangle Congruence Theorems

Hello!

This student-centered activity is an assessment of the identification and use of different theorems which can prove the congruence between two triangles. Specifically, we will be discussing three congruence postulates: 1. SAS (Side-Angle-Side) 2. ASA (Angle-Side-Angle) 3. SSS (Side-Side-Side)

Learning Competencies

At the end of the activity, the student will be able to… [M8GE-IIId-1] illustrate triangle congruence [M8GE-IIId-e-1] illustrate the SAS, ASA, and SSS congruence postulates [M8GE-IIIg-1] prove two triangles are congruent.

Si Mr. Right ka ba?

Just like Kim Chiu, we'll be looking for our own soulmates. Though, not our own soulmates, but that of triangles. In this activity, we'll be talking about congruent triangles, how to find out if two triangles are congruent using three postulates, and then solve for the missing values of triangles. Are you ready? Let's start!

What is Congruency?

Congruency When two shapes are of the same shape and size, we can consider them congruent. In this activity, we will be focusing on Congruent Triangles. You can use three postulates in determining if two triangles are congruent: The SAS (Side-angle-side) postulate, the ASA (Angle-side-angle) postulate, and the SSS (Side-side-side) Postulate.

SAS Postulate

Two triangles can be considered congruent if two known side lengths and their included angle measure are equal respectively to two side lengths and the included angle of the other triangle. (Africk, 2020)

SAS Simulation (Brezinski, n.d.-b)

ASA Postulate

Two triangles can be considered congruent if two known angle measures and their included side’s length are equal respectively to two angle measurements and the included side length of the other triangle. (Africk, 2020)

ASA Simulation (Brezinski, n.d.-a)

SSS Postulate

Two triangles can be considered congruent if three of the side lengths of one triangle are equal respectively to three of the side lengths of the other triangle. (Africk, 2020)

SSS Simulation (Brezinski, n.d.-c)

Now that we know the three postulates (SAS, ASA, and SSS), we can apply these in examining different triangles to see if they are congruent.

Questions

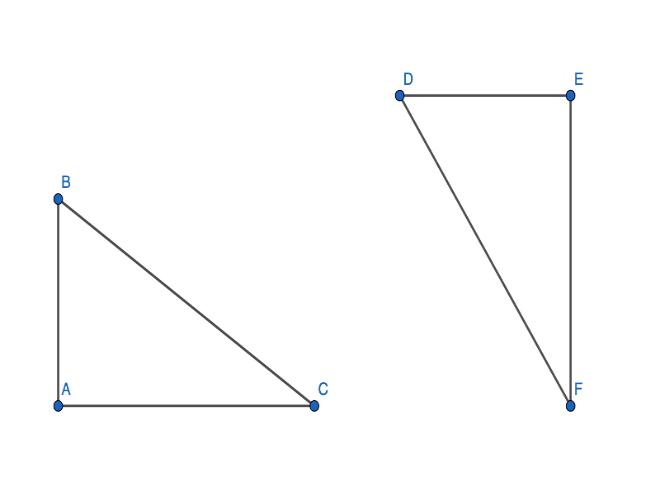
Q1.

You know that side AB is proportional to side DE. You also know that side AC is proportional to side EF. This is the only given information. Can you use a postulate to prove that triangle ABC and triangle DEF are congruent? If so, which postulate can you use to prove that triangle ABC is congruent to triangle DEF? If not, why not?

Q2.

You know that the measure of angle ABC is equal to the measure of angle EDF. You also know that the measure of angle ACB is equal to the measure of angle EFD. You also know that the measure of angle BCA is equal to the measure of angle DEF. This is the only given information. Can you use a postulate to prove that triangle ABC and triangle DEF are congruent? If so, which postulate can you use to prove that triangle ABC is congruent to triangle DEF? If not, why not?

Q3.

You know that side AB is proportional to side DE. You also know that side AC is proportional to side EF. You also know that side BC is proportional to side DF. This is the only given information. Can you use a postulate to prove that triangle ABC and triangle DEF are congruent? If so, which postulate can you use to prove that triangle ABC is congruent to triangle DEF? If not, why not?

Q4.

You know that the measure of angle ABC is equal to the measure of angle EDF. You also know that the measure of angle ACB is equal to the measure of angle EFD. You also know that the side length of BC is equal to the side length of DF. This is the only given information. Can you use a postulate to prove that triangle ABC and triangle DEF are congruent? If so, which postulate can you use to prove that triangle ABC is congruent to triangle DEF? If not, why not?

Q5.

You know that the measure of angle ABC is equal to the measure of angle EDF. You also know that the side length of BC is equal to the side length of DF. This is the only given information. What piece/s of information is missing in order to prove the congruency of triangle ABC and triangle DEF using the SAS postulate?

Q6.

References

Africk, H. (2020). 2: Congruent Triangles. In Elementary College Geometry. New York, NY: New York City College of Technology at CUNY Academic Works. Retrieved from https://math.libretexts.org/Bookshelves/Geometry/Book%3A_Elementary_College_Geometry_(Africk)/02%3A_CONGRUENT_TRIANGIES Brezinski, T. (n.d.-a). ASA Theorem?. Retrieved from https://www.geogebra.org/m/WKJJ2uPa Brezinski, T. (n.d.-b). SAS: Dynamic Proof! Retrieved from https://www.geogebra.org/m/bM5FkyFK Brezinski, T. (n.d.-c). SSS: Dynamic Proof! Retrieved from https://www.geogebra.org/m/Qsk3vDs6P