Primitiva funktioner
- Författare/skapare:
- Mathias Armbäck
- Område(n):
- Funktioner
Ibland kan man behöva veta vad något kommer från. Säg att vi ser en förändring men vill veta var den kommer i från.
Då tar vi reda på den primitiva funktionen. Det är som att derivera baklänges.
Vi vet att:
Men om vi bara har derivatan, så måste vi kunna gå baklänges.
Då gäller det att tänka på vad som hänt när man tar fram derivatan.
Till att börja med så kan man säga att man tar bort ett x från alla ställen.
Det skulle i så fall innebära:
Men sedan så tar man ju och multiplicerar med värdet hos exponenten när man deriverar. Då får man dividera med exponentens värde. Då borde de innebära:
Men när man deriverar och bara har en konstant då tar man ju bort den. Så om vi deriverar baklänges måste vi lägga till konstant. Nu vet vi ju inte vilken konstanten är så då får vi sätta dit en bokstav. ofta används C.
Detta är ju väldigt likt det vi började med, fast vår 8 har blivit ett C.
Det är i alla fall en grundläggande princip eller tanke man kan använda.
Mer formellt skriver man en primitiv funktion med versal.
eller
är en primitiv funktion till om .
För att ta reda på konstanten C behöver man känna till mer eller veta några egenskaper.
Säg att vi ska bestämma den primitiva funktionen till så att .
Vidare gäller då:
Men:
Så att:
Kul-problem
Jag stötte på ett kul problem om kulor på ett matematikforum för flera år sedan.
Man skulle ta reda på en formel för att beräkna antal kulor i en viss nivå av figur om man byggde dem som i en pyramid. Det kom in många avancerade svar och lösningar på forumet som jag inte förstod.
Jag löste den genom ett tänk med derivata och primitiva funktioner. Min lösning mottogs mycket varmt som en bra enkel lösning.
Nedan finns en skiss för en enklare version av problemet, man bygger som i en triangel, en 2D pyramid i stället för 3D. Men principen är den samma.
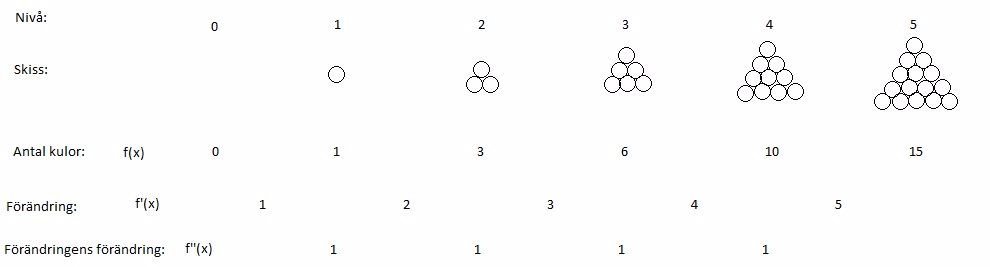
Lösningen gick ut på att ta reda på hur många kulor det fanns i de första figurerna och sedan kolla på hur det förändras och hur förändringen förändras.
När man kommer i detta fallet till andraderivatan är förändringen 1 hela tiden.
Då vet vi att
Då kan vi ta reda på derivatan som är en primitiv funktion till derivatan:
Nu kan vi ta reda på funktionen på samma sätt:
Nu tar vi reda på konstanterna genom att sätta in information vi känner till. Exempelvis vet vi att vid nivå 0 är där 0 kulor:
Sedan kan vi sätta i för nivå 1 ger 1 kula:
Då kan vi skriva och snygga till det:
Vi testar 5 kulor:
Det verkar ju stämma.