Modellrechner 4 zum Querdenken-Flugblatt von Dr. B. Schiffmann
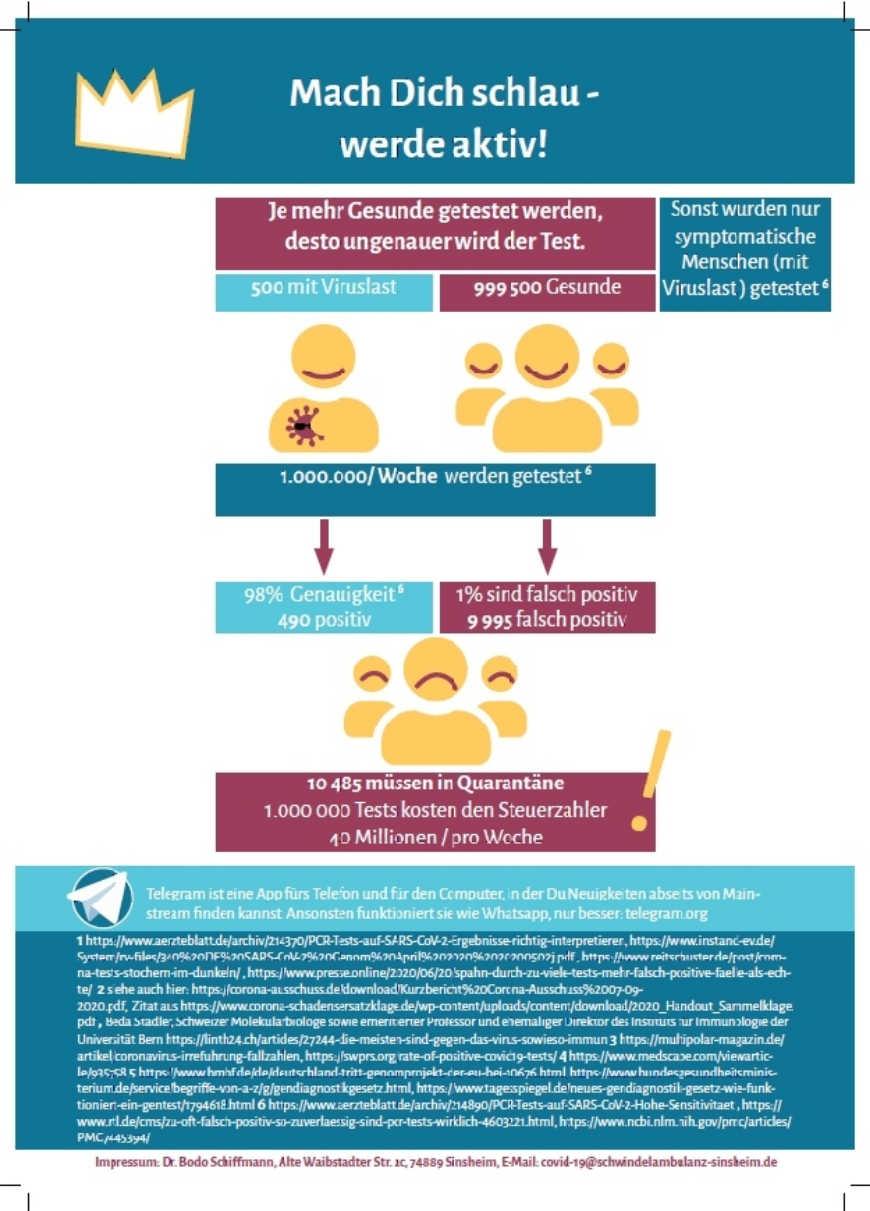
Ende Oktober 2020 gab es eine bundesweite Flugblatt Aktion von Dr. B. Schiffmann unter dem Titel "Coronas scharfe Kurven", in meinem Briefkasten am 31.10.2020.
Zu diesem Flugblatt gibt es eine an dessen Struktur angepasste Version des Corona-Modellrechners.
Eingaben sind hier in den grünen Feldern möglich.
Zunächst sind die Parameter von Dr. Schiffmann eingetragen:
Prävalenz: 500 Infizierte entspricht p = 0.0005 = 0.05 %, Spezifität = 0.99 = 99%, Sensitivität = 0.98 = 98%.
Ändern Sie diesen Wert auf 1% = 0.01, auf 2% = 0.02, auf 5% = 0.05, auf 10% = 0.1, auf 20% = 0.2.
Die Sensitivität setzt Dr. Schiffmann mit 98% an und die Spezifität mit 99%, auch wenn die Begriffe bei nicht ausdrücklich vorkommen und nicht deutlich unterschieden werden.
Die Spezifität besagt, mit welcher Wahrscheinlichkeit bei einer großen Stichprobe ein Infizierter auch korrekt als positiv erkannt wird.
Die Sensitivität besagt, mit welcher Wahrscheinlichkeit bei einer großen Stichprobe ein Nicht-Infizierter auch korrekt als negativ erkannt wird.
Die Prävalenz (Vorwahrscheinlichkeit, Positivenquote) kommt im Flugblatt nicht ausdrücklich als Wert vor und wird nicht thematisiert. Es werden einfach 500 Infizierte angesetzt. Das entspricht auf 1 000 000 Tests einem höchst ungewöhnlichen Prävalenz-Wert von 0.00005 = 0.05%.
Auf der Rückseite des Flugblatts ist demgegenüber von einer normalen 'Positivenquote' von 0.5 - 1.7% die Rede (also vom Zehn- bis über Dreißigfachen).
Das Ärzteblatt vermutet sogar weltweit 3% Prävalenz, das wäre das Sechzigfache des von Dr. Schiffmann benutzten Wertes.
Das ist insofern extrem wichtig, weil der positiv prädiktive Wert PPW (man könnte es umgangssprachlich auch 'Trefferquote' nennen) davon stark abhängt.
Während Spezifität und Sensitivität statistische Kennzahlen des Tests als solchem sind, gibt der PPW eine Aussage, mit welcher Wahrscheinlichkeit eine Einzelperson, die ein positives Testergebnis bekommen hat, auch tatsächlich infiziert ist. PPW und Spezifität werden in der Diskussion um Genauigkeit und Zuverlässigkeit häufig verwechselt und vermengt.
Bei einer Prävalenz von 0.0005= 0.05 % erhält man PPW = 4.7%, also nur etwas jeder Zwanzigste!
Bei einer Prävalenz von 0.01 = 1% wäre der PPW = 49,7%, also etwa jeder Zweite.
Bei einer Prävalenz von 0.017 = 1.7% wäre der PPW = 62.9%, also schon fast zwei von drei.
Bei einer Prävalenz von 0.1 = 10% wäre der PPW = 91.6%, also schon mehr als 9 von 10.
Was folgt daraus? Vor allem, dass die von Politikern gerne erhobene Forderung, möglichst viel zu testen, nicht sinnvoll ist, weil man dadurch zwar durchaus mehr positive Personen entdeckt, aber sich umso mehr falsch-positive einhandelt. Die Aussage von Dr. Schiffmann "Je mehr Gesunde getestet werden, desto ungenauer wird der Test" ist nicht ganz richtig, weil Sensitivität und Spezifität des Test sich dadurch nicht ändern. Sie hat aber auch einen wahren Kern, nämlich dass der PPW schlechter wird, wenn mehr Gesunde getestet werden. Deswegen ist die sinnvolle Schlussfolgerung auch nur, sich auf Testgruppen mit einer höheren Prävalenz (also Personen mit Symptomen) zu beschränken, anstatt mit Horrorzahlen über unnötige Quarantäne aufgrund extremer Annahmen über die Prävalenz Stimmung zu machen.
Flugblatt Corona Info Tour, Seite 2