Dominio, codominio e imagen
Una función, f, es una ley entre dos conjuntos de números: el dominio y el codominio. A cada número del dominio le hace corresponder un único número del codominio. Esta ley es una correspondencia unívoca.
Ejemplo:
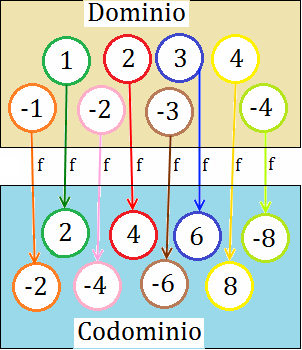En el ejemplo, el dominio es
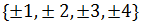El codominio es
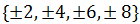Y la exprsión de la función es
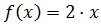ya que lo que hace la función es multiplicar por dos cada número del dominio.
Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.
Imagen o Recorrido
Sea x un elemento del dominio, llamamos imagen de x mediante la función f a f(x), es decir, al elemento del codominio que le asigna la función f.
Ejemplo: en la función del ejemplo anterior, la imagen de 1 es f(1)=2, la imagen de -2 es f(-2)=-4.
Llamamos conjunto imagen (o simplemente imagen) o recorrido de la función f al conjunto de elementos del codominio que son la imagen de algún (o más) elemento del dominio.
Es decir, si y es un elemento de la imagen de f, entonces existe al menos un elemento, x, del dominio de f tal que
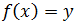Ejemplo 1
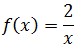Dominio: como es una función racional, tenemos que excluir del dominio los puntos que hacen que el denominador sea 0 (no podemos dividir por 0). Por tanto, el dominio es
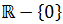Recorrido: El recorrido es todos los reales excepto 0 ya que si suponemos que
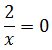entonces
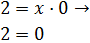Lo cual es falso. Esto quiere decir que la ecuación no tiene solución y, por tanto, el 0 no tiene antimagen (elemento del dominio cuya imagen es 0).
Por tanto, la imagen de f es
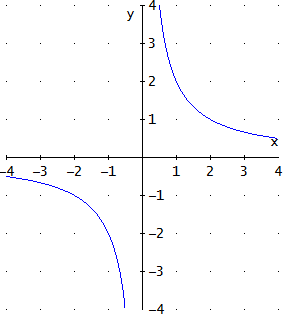
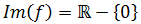La gráfica es:
Ejemplo 2
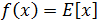Esta función es la parte entera de x. Lo que hace es quitar la parte decimal del número y quedarse con la parte entera. Por ejemplo,
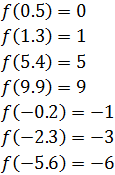Dominio: el dominio de la función es todos los reales.
Recorrido: Es fácil ver que la imagen de la función es el conjunto de los números enteros:
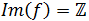donde
La gráfica es:
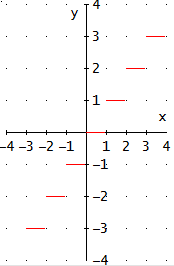Más Ejemplos
Enlace: Ejercicios resueltos: cálculo del dominio y recorrido de funciones de una variable real
Enlace relacionado: Ejercicios resueltos: estudio de la continuidad de funciones de una variable real
Enlaces:
En el ejemplo, el dominio es
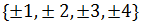El codominio es
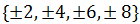Y la exprsión de la función es
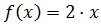ya que lo que hace la función es multiplicar por dos cada número del dominio.
Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.
Imagen o Recorrido
Sea x un elemento del dominio, llamamos imagen de x mediante la función f a f(x), es decir, al elemento del codominio que le asigna la función f.
Ejemplo: en la función del ejemplo anterior, la imagen de 1 es f(1)=2, la imagen de -2 es f(-2)=-4.
Llamamos conjunto imagen (o simplemente imagen) o recorrido de la función f al conjunto de elementos del codominio que son la imagen de algún (o más) elemento del dominio.
Es decir, si y es un elemento de la imagen de f, entonces existe al menos un elemento, x, del dominio de f tal que
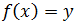Ejemplo 1
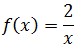Dominio: como es una función racional, tenemos que excluir del dominio los puntos que hacen que el denominador sea 0 (no podemos dividir por 0). Por tanto, el dominio es
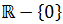Recorrido: El recorrido es todos los reales excepto 0 ya que si suponemos que
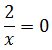entonces
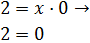Lo cual es falso. Esto quiere decir que la ecuación no tiene solución y, por tanto, el 0 no tiene antimagen (elemento del dominio cuya imagen es 0).
Por tanto, la imagen de f es
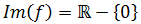La gráfica es:
Ejemplo 2
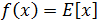Esta función es la parte entera de x. Lo que hace es quitar la parte decimal del número y quedarse con la parte entera. Por ejemplo,
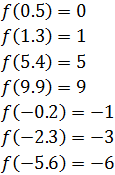Dominio: el dominio de la función es todos los reales.
Recorrido: Es fácil ver que la imagen de la función es el conjunto de los números enteros:
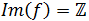donde
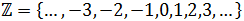La gráfica es:
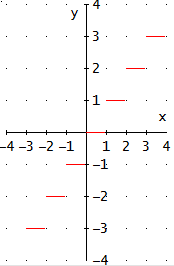Más Ejemplos
Enlace: Ejercicios resueltos: cálculo del dominio y recorrido de funciones de una variable real
Enlace relacionado: Ejercicios resueltos: estudio de la continuidad de funciones de una variable real
Enlaces: