Diskontinuerliga funktioner
Om en graf är sammanhängande inom ett intervall då är den kontinuerlig.
Om det finns "hopp" eller "skarvar" inom ett intervall då är den diskontinuerlig.
Ett sätt som man kan tänka är om grafen går att rita "utan att lyfta pennan" eller inte.
Försök att "sätta ihop" graferna så att den blir kontinuerlig
I appletten ovan har vi f som är definierad på följande sätt:
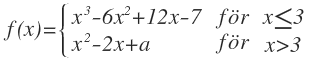
Låt oss ta reda på för vilket a som f blir kontinuerlig.
Vi vet att de måste ha samma värde då x=3 för att vara kontinuerliga.
Vi börjar med att beräkna värdet den lägre delen har då x=3 så att vi kan ta reda på vilket a ger samma värde för den högre delen.
Då löser vi a från den högre delen vid samma x värde och samma funktionsvärde.
f blir kontinuerlig då a=-1.