Funktionen
Was ist ein Funktion:
Eine Funktion (Abbildung) f ist eine eindeutige
Zuordnung, die jedem Wert x in eindeutiger Weise einen Funktionswert y
zuweist.
stehen aus 3 komponenten:
· Eine Menge D, aus der die Werte der unabhängigen Variablen genommen werden dürfen (die Definitionsmenge),
· eine Menge W(Wertmenge) welche teilmenge von Z, in der alle Funktionswerte liegen
(die Zielmenge)
· und schließlich eine Vorschrift, die jedem Element der
Definitionsmenge D in eindeutiger Weise ein Element der Zielmenge Z zuordnet.
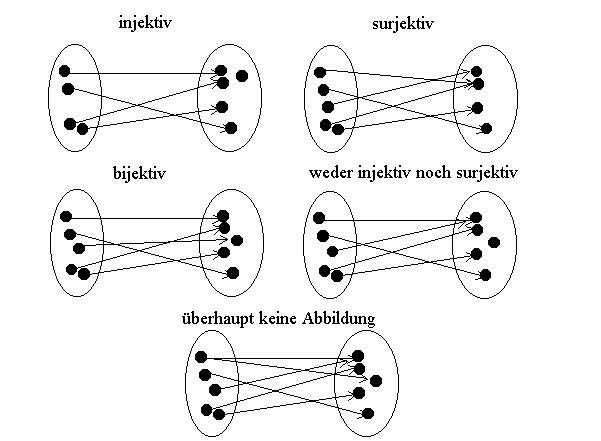
Funktionstypen:
· surjektive Funktion: Zu jedem Element der Zielmenge führt mindestens ein Pfeil
· injektive Funktion: Zu jedem Element der Zielmenge führt höchstens ein Pfeil
· bijektive Funktion: Zu jedem Element der Zielmenge führt genau ein Pfeil
Wann handelt sich um keine Funktion:
· Es handelt sich um keine Funktion, da die Stelle 2 auf zwei
Funktionswerte abgebildet wird. Diese Zuordnung ist nicht eindeutig.
(Interpretation in einer Anwendung: Eine bestimmte Menge x eines
Produkts kann – unter normalen Verhältnissen – nicht zwei verschiedene Preise y
haben.)
FUNKTIONEN (Prof. Lindner): https://www.geogebra.org/m/ZqwHdb9Y
Funktionstypen