EPT - Harmonischer Oszillator
Mit freundlicher Genehmigung von Michael Rode.
Grundgedanken
Die Einführung eines variablen Potenzials in den EPT mit unendlich hohen Wänden erweist sich in der Umsetzung in die Zeigerdarstellung als sperrig. Vorliegende Versuche müssen daran scheitern, dass es wegen der UBR nicht erlaubt ist, dem Elektron an einem Beobachtungsort eine scharf festgelegte Wellenlänge zuzuweisen.
Den sich daraus ergebenden „gordischen Knoten“ durchschlägt man einmal mehr durch sorgfältiges Nachdenken über die Superposition: für jede Denkmöglichkeit einen Zeiger.Das Modell Harmonischer_Osz soll ein erfolgreiches Vorgehen darstellen und verstehen helfen.
Leitfrage: „Worin besteht die Unkenntnis, als deren Folge zu superponieren ist?“
Der hier verfolgte Ansatz behält einerseits die Unkenntnis über die Lage der Quelle (links bzw. rechts) bei, wie bei der Modellierung des Elektrons im EPT. Andererseits besteht bei festliegender Gesamtenergie des Elektrons („stationärer Zustand“) aber Unkenntnis über die Verteilung auf potenzielle Energie und kinetische Energie des Elektrons. Dadurch müssen mehr als zwei Denkmöglichkeiten in die Superposition einbezogen werden. Die Gesamtenergie wird festgelegt durch das quadratische Potenzial. Diese Gesamtenergie stimmt mit der potenziellen Energie am Rand des Oszillators überein. Variable Gesamtenergie zeigt sich dann im Modell durch ebenfalls variablen Radius des Oszillators. Abhängig vom Ort ergibt sich die für die Wellenlänge maßgebliche kinetische Energie als Differenz der ortsabhängigen potenziellen Energie und der Gesamtenergie. Damit stehen über die deBroglie-Relation die Wellenlängen Lamda1..Lambda5 der zu superponierenden Zeiger fest. Man müsste für jeden Ort im Bereich des Oszillators einen Zeiger berechnen. Es hat sich in der Praxis bewährt, mit 5..7 Orten zu arbeiten, wie das Gesamtergebnis zeigen wird. Im vorliegenden Modell werden 5 Orte P1..P5 gleichmäßig auf den Durchmesser des Oszillators verteilt. Die Definitionen für die verwendeten Elemente können in der linken Spalte des GeoGebra-Modells nachgelesen werden.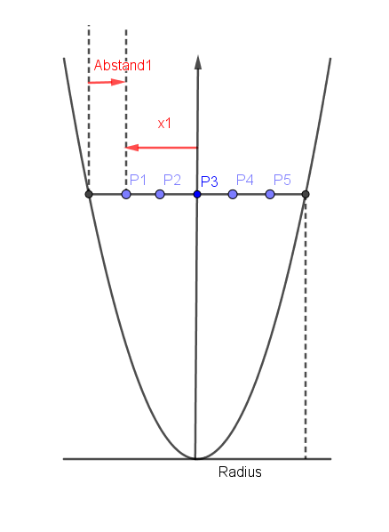
;
;
- Amplituden 0,25;1;1,75;1;0,25
Einführung von Gewichtungsfaktoren
Eine genauere Auseinandersetzung mit der Modellierung bei der Konstruktion des Modells machte deutlich,
dass die verwendeten Zeiger nicht alle gleich lang sein dürfen.
Die Nachweiswahrscheinlichkeit des betrachteten Elektrons wird nicht in allen Intervallen gleich groß
sein.
Deswegen werden Gewichtungsfaktoren eingeführt, denen die Annahme zu Grunde liegt, dass die Nachweiswahrscheinlichkeit quadratisch mit dem Abstand zur Mitte abnehmen wird. Der erste, im Modell rotbraun dargestellte Zeiger erhält willkürlich die Länge 0,25. Die Gewichte der folgenden sind 1; 1; 1,75; 1; 0,25.
Handhabung des Modells
Man vergrößert den Radius mit Hilfe des Schiebereglers, jeweils bis am rechten Rand ebenfalls ein Knoten
vorliegt, die Randbedingung „Nachweiswahrscheinlichkeit = 0“ also erfüllt ist.
Man notiert die Anzahl n der dabei auftretenden Peaks und die Gesamtenergie.
Messbeispiel (Eges in willkürlichen Einheiten angegeben):
| n | Eges |
| 1 | 156 |
| 2 | 310 |
| 3 | 460 |
| 4 | 602 |
| 5 | 749 |
| 6 | 895 |
| 7 | 1030 |
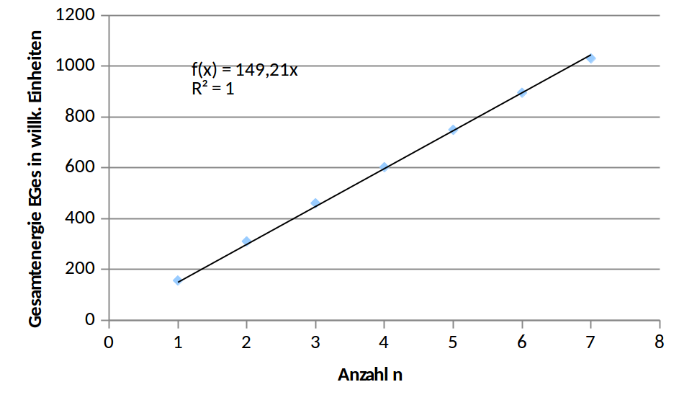
Die Übereinstimmung mit den Erwartungen: „Gesamtenergie proportional zu n“ wird hervorragend bestätigt, was als Beleg dafür gewertet wird, dass die Darstellung der Superposition im Modell angemessen gewählt wurde.
