L4.9 - Using Trigonometric Ratios to Find Angles
Learning Intentions and Success Criteria
We are learning to:
- Calculate angle measures in right triangles using arccosine, arcsine, and arctangent
- Use arccosine, arcsine, and arctangent to find angle measures in right triangles
9.1: Once More with the Table
A triangle with side lengths 3, 4, and 5 is a right triangle by the converse of the Pythagorean Theorem. What are the measures of the acute angles?
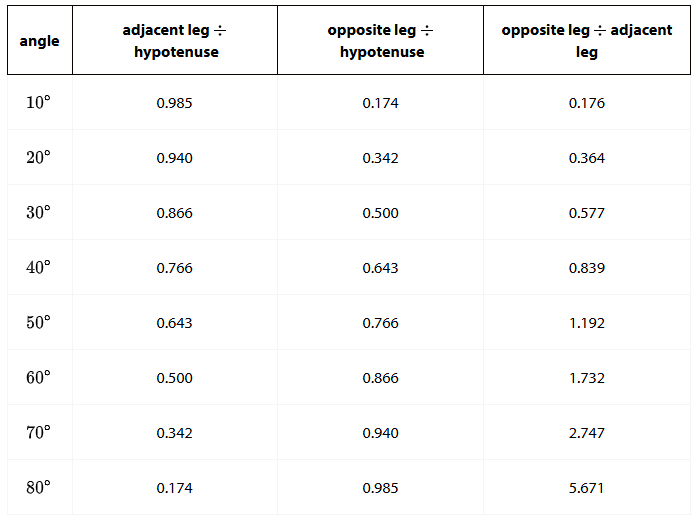
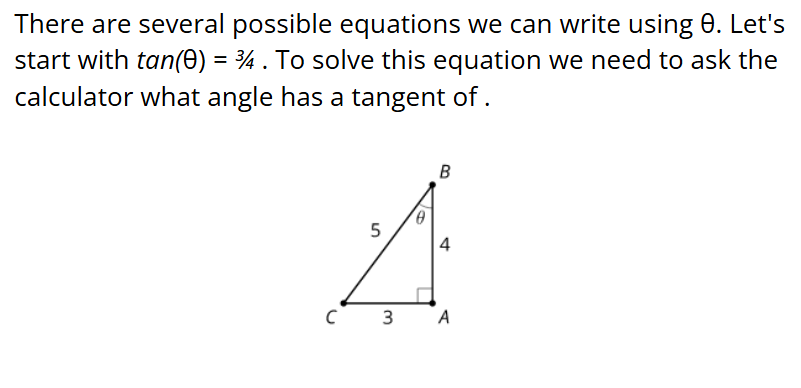
tan() = To solve this for angle degree use tan(3/4) on the calculator is also called arctangent.
9.2: From Ratios to Angles
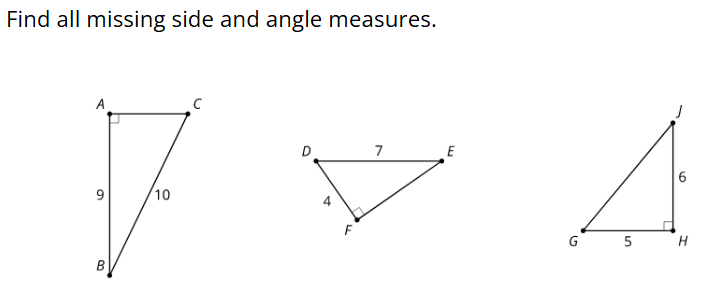
ABC
DEF
GHJ

Learning Intentions and Success Criteria
We are learning to:
- Calculate angle measures in right triangles using arccosine, arcsine, and arctangent
- Use arccosine, arcsine, and arctangent to find angle measures in right triangles
Cool-Down: Again with the Calculator
A triangle with side lengths 8, 15, and 17 is a right triangle by the converse of the Pythagorean Theorem. What are the measures of the other 2 angles?