Construcción de un polígono regular
NOTA INICIAL
Ejercicio 13 del CURSO DE INICIACIÓN A GEOGEBRA
Esta es una construcción aproximada, siguiendo la idea de construcción con regla y compás sugerida en los manuales de geometría práctica (más detalles en esta página de Gaussianos.com)
Otro análisis de esta aproximación la muestra Ignacio Larrosa Cañestro en esta página
Construcción de un heptágono
- Dibujamos la circunferencia c que pasa por los puntos A y B, usando
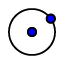. - Con
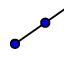trazamos la semirrecta a con origen en B que pasa por A. - Seleccionamos un punto C de la circunferencia c.
- Trazamos la semirrecta b con origen en B que pasa por C.
- Seleccionamos un punto D de la semirrecta b.
- Dibujamos la circunferencia d con centro en D que pasa por B.
- Calculamos el punto E, intersección de la circunferencia d con la semirrecta b.
- Trazamos la circunferencia e con centro en E que pasa por D.
- Repetimos los pasos anteriores dependiendo del n° de lados que tenga el polígono regular que queremos construir. En este caso es un heptágono, por lo que aparte de C y D necesitamos 6 nuevos puntos: sobre la semirrecta b obtenemos los puntos D, E, F, G, H, I y J.
- Calculamos el punto de corte K de la circunferencia c y la semirrecta a.
- Con
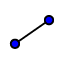unimos mediante un segmento el punto J con el punto K.
- Trazamos paralelas al segmento anterior que pasen por los puntos determinados sobre la semirrecta b usando
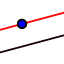. Calculamos los puntos de corte de estas rectas paralelas con la semirrecta a. Obtenemos los puntos L, M, N, O, P y Q.
- Trazamos la circunferencia con centro en K que pasa por B y la circunferencia con centro en B que pasa por K.
- Calculamos el punto de corte de ambas circunferencias, R.
- Trazamos la semirrecta f1 con origen en R que pasa por M.
- Calculamos el punto de corte S de la semirrecta f1 con la circunferencia c.
- Trazamos el segmento de extremos B y S. Este segmento es el lado del polígono regular.
- Mediante circunferencias, calculamos el resto de los vértices del polígono.
- Unimos los vértices mediante la herramienta polígono
.