L7.3 - Tangent Lines

Learning Intentions and Success Criteria

We are learning to:

Use the relationship between tangent lines and radii to prove (using words and other representations) a theorem about circumscribed angles.

We are successful when we can:

Use the relationship between tangent lines and radii to calculate angle measures and prove geometric theorems.
Know that a line tangent to a circle is perpendicular to the radius drawn to the point of tangency.

3.1: Swim to Shore

Line l represents a straight part of the shoreline at a beach. Suppose you are in the ocean at point C and you want to get to the shore as fast as possible. Assume there is no current. Segments CJ and CD represent 2 possible paths.

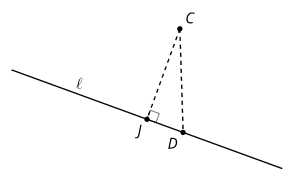
Diego says, “No matter where we put point D, the Pythagorean Theorem tells us that segment CJ is shorter than segment CD. So, segment CJ represents the shortest path to shore.” Do you agree with Diego? Explain your reasoning.

3.2: A Particular Perpendicular

Draw a radius in the circle. Mark the point where the radius intersects the circle and label it A.
Construct a line perpendicular to the radius that goes through point A. Label this line n.
Line n intersects the circle in exactly 1 point, A. Why is it impossible for line n to intersect the circle in more than 1 point?

4. What kind of line, then, is n?

3.3: Another Angle

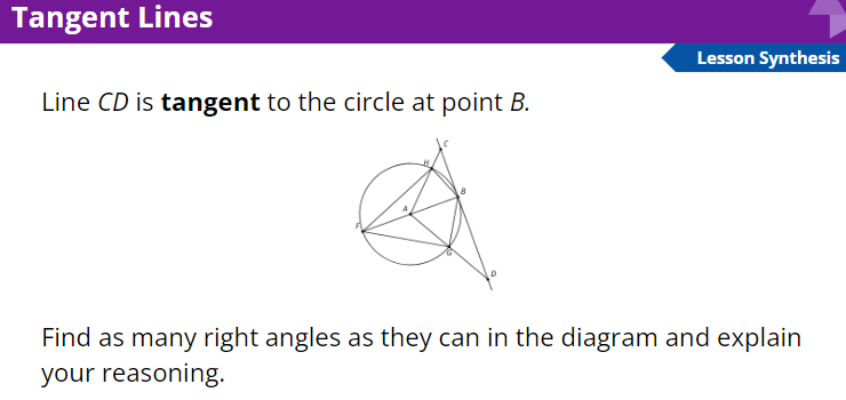
The image shows an angle whose rays are tangent to a circle.

Mark the approximate points of tangency.
Draw the 2 radii that intersect these points of tangency. Label the measure of the central angle that is formed w.
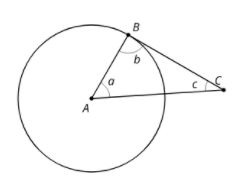
What is the value of w + z? Explain or show your reasoning.

Learning Intentions and Success Criteria

We are learning to:

Use the relationship between tangent lines and radii to prove (using words and other representations) a theorem about circumscribed angles.

We are successful when we can:

Use the relationship between tangent lines and radii to calculate angle measures and prove geometric theorems.
Know that a line tangent to a circle is perpendicular to the radius drawn to the point of tangency.