群のパズル
1.平面色塗りパズルで構造をつかもう
このワークシートはMath by Codeの一部です。
<円順列を群論で求めよう>
例えば、「正方形の4個の頂点に白か黒の玉を置く円順列を求める」問題について調べてみよう。
この問題は、正方形の頂点にたとえば左かどから反時計回りに1,2,3,4と番号をふり、その番号の玉が
◯ならば0、⚫️ならば1を割り当てると、2の4乗=16通りの配置が可能になる。
この配置の集合をX={x1,x2,.....,x16}とするとき、
正方形を90度反時計周りに回転する操作をrとして、回転の群G={e, r, r2,r3}による働きで同値になるものを1つと数える、つまり、同値類の数を求める問題になる。
仕組みをさぐるために、同値類の数から逆にXとGの関係性から規則性を詳細にしらべてみよう。
同値類の6個あり、以下はその代表元だ。
C1 C2 C3 C4 C5 C6
◯◯ ◯◯ ◯◯ ◯● ●● ●●
◯◯ ◯● ●● ●◯ ◯● ●●
では、Xの1,2,3,4の要素に対する0,1の値を座標のようにタプルを値として表してみよう。
Xの要素であることがわかるようにxに添え字をつけて、キーとして辞書のようにメモしておこう。
C1={x1:(0,0,0,0)}
C2={x2:(1,0,0,0), x3:(0,1,0,0), x4:(0,0,1,0), x5:(0,0,0,1)}
C3={x6:(1,1,0,0), x7:(0,1,1,0), x8:(0,0,1,1), x9:(1,0,0,1)}
C4={x10:(1,0,1,0), x11:(0,1,0,1)}
C5={x12:(0,1,1,1), x13:(1,0,1,1), x14:(1,1,0,1), x15:(1,1,1,0)}
C6={x16:(1,1,1,1)}
まず、同値類のすべてのx∈Ciにすべてのg∈Gを作用させたときの安定数(g,x)の合計する。
安定数(g,x)とは、xがgで動かない(g*x=x)ときだけ1、他のXの位置に動いたら0と定める。
C1なら、x1はGの4つの要素のどれでも動かないから、1+1+1+1=4になる。
C2のとき、x2,x3,x4,x5のどれも回転で動いていしまうので、eの作用のときだけ安定するから1×4=4。
C3のときもC1と同様にして4。
C4のときは0回転か180度回転かだけ動かないので、x10に対してe,r2, x11に対してもe,r2のときの4通りだけ1になるから和は4になる。
C5のときは、C2と同じ理由で4。
C6のときはC1と同じ理由で4。
こうしてみると、どの同値類ごとの安定数(g,x)の合計は4だから、
★安定数の総和=4×6=Gの位数×同値類の数=24
となった。
なぜ、同値類ごとの安定数(g,x)の合計がいつもGの位数4になるのだろうか。
前回、
(群のサイズ)=(xの安定化群のサイズ)×(xの軌道サイズ)
を知りました。
(※これは軌道―安定化群定理とか、軌道ー固定部分群定理とかOS定理と呼ばれたりします。)
ここで、(xの軌道サイズ)を(同値類のサイズ)と読み替えると、
C1,C6では、4×1=4になっていて、
C2,C3,C5では、1×4=4になっていて、
C4では、2×2=4になっていることがわかるね。
この安定数(g,m)の計算結果表を0を省略してかいてみよう。
同値類 C1 C2 C3 C4 C5 C6
X 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
G e 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
r1 1 1
r2 1 1 1 1
r3 1 1
1が24個ならんでいるはずだね。
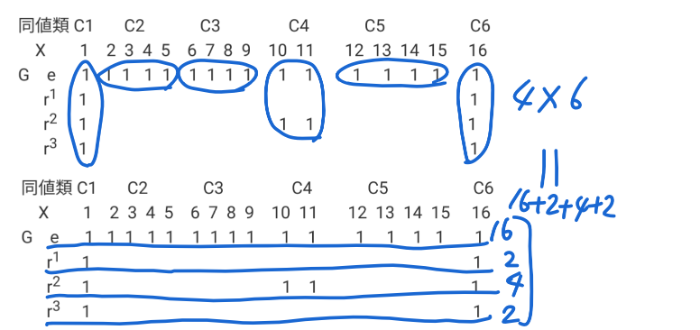
ここで視点をかえよう。
1か0かを判断するには同値類ごとにたてに調べるのではなく、作用Gの要素ごと1行ずつでもできる。
eによる安定数はすべて1になるから、1が16個できるから合計は16。
r1による安定数は90度回転で不変な配置はx1,x16の2個だけだから、合計は2個
r2による安定数は180度回転で不変な配置だから、x1,x16の他にx10,x11があり、合計4になる。
r3による安定数は270度回転で不変な配置だからx1,x16で合計2。
注意:(Xの要素16個の割り当ては、同値類との対応がわかるように配置を決めてしまっているけれど、
行単位、つまり作用する群Gの要素単位での計算にはまったく関係しないし、どの配置をxの何番にするかという、初期設定とは無関係に求めることができることを確認しよう。)
★安定数の総和=16+2+4+2=24
=Gの各元gごとの安定数の和の合計={(g,x)|gx=x}の個数
以上2つの★を1つにまとめると、
(16+2+4+2)/4=6と円順列数が計算できるはずだ。
まとめると、
円順列数(回転による同値類数)=sum(sum(安定数 for x ∈X)for g ∈G)/|G|
(一般化)
群Gが集合Xに作用するとき、
関数(g,x):=1 if g*x=x else 0 と定義すると、
同値類の総数=sum(sum(g,x)x ∈X)g ∈G /|G|
となる。
これをバーンサイドの公式、コーシー-フロベニウスの公式と呼ぶ人もいる。
<公式を使ってみよう>
質問:正六角形の頂点に白3個、黒3個の玉を並べる円順列はどうやって求められますか。
直線的に並べると1番から6番までの番号から白の番号3個を選ぶと6C3=20通りです。
配置を、◯を0,⚫️を1として1番目から6番目に0と1を3個ずつならべた数で表そう。
X={x1:000111, x2: 100011, x3: 110001, x4:111000,x5:011100,x6:001110, .......x20:010101}などと
配置リストを作ろう。|X|=20だね、
正6角形を60度回転する操作をrとして、回転の群G={e, r1,r2,r3,r4,r5}で、|G|=6です。
回転群の要素ごとにsum(安定数)を求めた総和を|G|で割ることで、同値類の数を求めよう。
e∈G のときはすべて不変だから、sum(安定数) = 20
r1,r3, r5∈GのときはXの要素で不変になるものはないからsum(安定数)=0。
r2,r4∈Gのときは1と0を交互に並べた配置が不変になりsum(安定数)=2+2=4。
だから、円順列数=sum(安定数)の総和/|G|=(20+4)/6=4と求められるね。
算数的にやると、◯と◯を隔てる⚫️の個数は1,1,1です。3=1+1+1ですね。
3の和分解に順列をからめる。
3=0+0+3→円に連結すると、◯◯◯●●●の1
0+1+2→円に連結すると、◯◯●◯●●、◯●◯◯●●の2
1+1+1→円に連結すると、◯●◯●◯●の1
だから、1+2+1=4通り。
<難易度をあげてみよう>
「正六角形の頂点に白か黒の玉をおく円順列」を求めよう。ぜんぶ白でも全部黒でもよいとする。
配置の集合Xのサイズは26=64通りあります。Xはxi={1:0/1, 2:0/1, 3:0/1, 4:0/1,5:0/1, 6:1/6}として、
0か1を重複して使う重複順列で64個の要素を作ることができます。
60度回転は6次の巡回置換r=(1,2,3,4,5,6)にして、回転群G={e, r, r^2, r^3,r^4, r^5}とします。
安定数の合計をGの要素ごとに求めましょう。
・sum((e,x))=|X|=64
・rでxの01配置は1つずつ進むため、すべて同じaaaaaa型だけ安定です。a=1,0だからsum=2。
・r^2でxの01配置は1つおきに進み、2個周期のababab型だ安定です。a,b=1,0の重複順列sum=2×2=4。
・r^3でxの01配置は2つおきに進み、3個周期のabcabc型が安定です。a,b,c=1,0の重複順列で2^3=8。
・r^4はr^2の逆回転だから、同じsum=4。
・r^5はrの逆回転だから、同じsum=2。
円順列=sum(安定数)の総和/|G|=(64+2+4+8+4+2)/6=84/6=14通り
一般化しよう。
対象の位置数をn, 配置する種類数をm, 作用する群Gの要素数を|G|とすると、
Xの要素はmのn乗ある。
安定数を求めるとGがeのときは、Xがすべて安定するから安定数sum((e,x))=|X|=m^nこれが0スロット型。
Gの要素でたがいに移り合うときはaaa...aa型だけ安定、aがm通りだからsum=m。これが1スロット型。
Gの要素が1つおきに進むなどしてabab..ab型など2文字選ぶ安定数sum=m^2。これが2スロット型。
2つおきに進むなどして3文字選ぶ安定数はsum=m^3。これが3スロット型。
上記の場合はm=2,n=6で、0スロット、1スロット、2スロット、3スロットの型順に
Gの要素が1,2,2,1ある。だから、
(2^6+2*2^1+2*2^2+1*2^3)/6で求められた。
n=6の場合、
円順列数=
(2m+2m2+m3+m6)/6=(2+2m+m2+m5)*m/6
で求められる。
質問:正六角形の頂点に白か黒の玉をおく円順列を計算だけで求めるにはどうしましょう。
Gsize=6として群のサイズを設定します。
作用する群の要素も、玉の配置も辞書として設定するとあとで扱いやすいです。
makeX(chara)関数でchara=[01]として、白黒を正六角形に並べる2の6乗の配置Xを生成しましょう。
itertoolsパッケージのproduct関数で簡単に重複順列は作れますが、辞書にしておくと群の作用の結果、
安定しているかどうかの確認が簡単にできますね。
con関数で回転の合成を辞書として返します。
gx関数でXの要素への作用結果を辞書として返します。
sumgx(g, X)は1つのgに対する安定数を求める関数です。
Gの各要素gについてsumgxを求めて合計し、それをGsizeで割ればよいね。
ami_goは、辞書にはすべてのキーを標準で設定しているのでかなり簡単になりました。
[IN]Python
#=========================================================
from itertools import product as pp
def ami_go(k,dic):
return dic[k]
def con(a,b):#a,bの順に連結したあとの辞書を返す。
global keys
return {key:ami_go(ami_go(key,a),b) for key in keys}
def gx(g,x):#gをxに作用させたあとの辞書を返す。
global keys
return {ami_go(key,g):ami_go(key,x) for key in keys}
def sumgx(g,X):
return len([x for x in X if gx(g,x)==x])
def makeX(chara):
global keys
rep = len(keys)
#charaを重複してrep個ならべる重複順列jjを作る
jj = list(pp(chara,repeat=rep))
#重複順列jjを1,2,3,4,5,6をキーにした辞書化する
jjdic=[dict(zip(keys,j)) for j in jj]
return jjdic
#=========ここからがデータ入力
Gsize=6
keys = list(range(1,Gsize+1))
e= {1:1, 2:2, 3:3, 4:4, 5:5,6:6}
r= {1:2, 2:3, 3:4, 4:5, 5:6,6:1}
r2=con(r,r)
r3=con(r2,r)
r4=con(r3,r)
r5=con(r4,r)
#作用する群G
G=[e,r,r2,r3,r4,r5]
#対象となる模様X
X=makeX([0,1])
sums=[sumgx(g,X) for g in G]
sumofsums= sum(sums)
print(f"sum of sums{sums} = {sumofsums}")
print(f"同値類数 = {sumofsums//len(G)}")
#====================================
[OUT]
sum of sums[64, 2, 4, 8, 4, 2] = 84
同値類数 = 14
<群論の威力を感じよう>
さらに難易度の高い問題に挑戦することで、群論のパワーを感じたい。
問題「六角形の頂点を重複を許して3種の色でぬるとき、(1)重複円順列と(2)重複じゅず順列の数を求めましょう」
(1)コードでやると、上記の[0,1]を[0,1,2]に変えるだけです。
[IN]Python
#===================================
X=makeX([0,1,2])
sums=[sumgx(g,X) for g in G]
sumofsums= sum(sums)
print(f"sum of sums{sums} = {sumofsums}")
print(f"同値類数 = {sumofsums//len(G)}")
#===================================
sum of sums[729, 3, 9, 27, 9, 3] = 780
同値類数 = 130
さっきの一般化を公式として使ってみましょう。
n=6、m=3の場合の円順列数=(2+2m+m2+m5)*m/6=(2+2*3+3^2+3^5)*3/6=(2+6+9+243)/2=130
(2)円順列をじゅず順列にするには、G=C6ではなく、6次の2面体群D6に変更する必要があります。
だから、Gに線対称移動のtを設定して、その軸をrで回転させたものを含めて6要素を群の要素に
追加しましょう。
#=========ここからがデータ入力
Gsize=6
keys = list(range(1,Gsize+1))
e= {1:1, 2:2, 3:3, 4:4, 5:5,6:6}
r= {1:2, 2:3, 3:4, 4:5, 5:6,6:1}
r2=con(r,r)
r3=con(r2,r)
r4=con(r3,r)
r5=con(r4,r)
t = {1:6, 2:5, 3:4, 4:3,5:2,6:1}
rt=con(r,t)
r2t=con(rt,r)
r3t=con(r2t,r)
r4t=con(r3t,r)
r5t=con(r4t,r)
#作用する群G
G=[e,r,r2,r3,r4,r5,t,rt,r2t,r3t,r4t,r5t]
#対象となる模様X
X=makeX([0,1,3])
sums=[sumgx(g,X) for g in G]
sumofsums= sum(sums)
print(f"sum of sums{sums} = {sumofsums}")
print(f"同値類数 = {sumofsums//len(G)}")
#====================================
[OUT]
sum of sums[729, 3, 9, 27, 9, 3, 27, 81, 27, 81, 27, 81] = 1104
同値類数 = 92
数珠順列の場合は線対称移動と反時計回り回転の合成で。作用は6種類増えます。
裏返し1回は3スロット型です。
裏返し1回のあとに60度回転をするとどうなるでしょう。
裏返しの対称軸をはさむのが1番と6番の位置としましょう。
裏返しで1と6の色は交換されますが、1番の色は60度回転でキャンセルされまてしまうのです。
1→6→1、6→1→2です。
残りは、2と5、3と4は交換されて60度回転で2→5→6,5→2→3, 3→4→5, 4→3→4。
つまり、{1:1, 4:4, 6:2, 2:6, 3:5, 5:3}となり、1と4を固定して、のこりを線対称移動します。
1と4は同色とは限らないので、スロットは4です。
こうして、裏返しと回転の合成は、対称軸の位置が60度ではなく30度ずつ移動することがわかります。
だから、スロット型は3,4,3,4,3,4となります。
まとめると、|G|=6+6=12です。
m=3,n=6で、0スロット、1スロット、2スロット、3スロット、4スロットの型順に
Gの要素が1,2,2,1+3=4, 3 ある。だから、円順列の公式を拡張することで、
(3^6+2*3^1+2*3^2+4*3^3+3*3^4)/12で求められるでしょう。
(3^6+2*3^1+2*3^2+7*3^3)/12
=(729+2*3+2*9+4*27+3*81)/12=(729+6+18+108+243)/12=92
です。
2.立方体の彩色をやってみよう
質問:立方体の頂点をm色で塗る数は何通りでしょうか。回転して重なる塗り方は1通りとします。
平面とのちがいは、群Gの種類が増えることだ。考え方は平面と同じだね。
n=8で、Gは正6面体群P6だからS4と同型で、4!=24個の要素がある。
・無回転の安定数はm^8。
・2対面の中心を結ぶ6÷2=3軸で90度の1,3倍回転は、軸に垂直な2面を色分けする。
スロットは2だから、安定数=6m^2
・2対面の中心を結ぶ6÷2=3軸で90度の2倍回転では、軸に垂直な2面の中で交互に色分けする。
スロットは2*2=4だから、安定数=3m^4
・対辺の中点どうしを結ぶ4×3÷2=6軸での180度回転では、軸に平行な2面が入れ替わる。
スロットは4、安定数=6m^4
・主対角線、4軸での120度の1、2倍回転する4×2=8個では、軸上の2点は別色でよく、残りは軸を回る
2つの軌道が別色でよいから、スロットは4、安定数=8m^4
P安定数の合計=(m^8+6m^2+3m^4+6m^4+8m^4)/4!=
これが、m色での塗り方の合計になるね。
m=2なら、
(m**8+6*m**2+3*m**4+6*m**4+8*m**4)//(4*3*2*1)=23通りだ。
質問:立方体の面をm色で塗る数は何通りでしょうか。回転して重なる塗り方は1通りとします。
平面とのちがいは、群Gの種類が増えることだ。考え方は平面と同じだね。
n=6で、Gは正6面体群P6だからS4と同型で、4!=24個の要素がある。
・無回転の安定数はm^6。
・2対面の中心を結ぶ6÷2=3軸で90度の1,3倍回転は、軸を通る2面と側面で3色に分けする。
スロットは3だから、安定数=6m^3
・2対面の中心を結ぶ6÷2=3軸で90度の2倍回転では、軸を通る2面と側面を2対面に色分けする。
スロットは2+2=4だから、安定数=3m^4
・対辺の中点どうしを結ぶ4×3÷2=6軸での180度回転では、軸からはなれた面と軸と辺で接する2組
の面で色分け スロットは3だから、安定数=6m^3
・主対角線、4軸での120度の1、2倍回転する4×2=8個では、軸にはしの頂点を共有する3面を1組で
で2色分け、スロットは2、安定数=8m^2
P安定数の合計=(m^6+6m^3+3m^4+6m^3+8m^2)/4!=
これが、m色での面の塗り方の合計になるね。
m=2のときは、
(m**6+6*m**3+3*m**4+6*m**3+8*m**2)//(4*3*2*1)=10通りとなる。