Applying Pythagoras Theorem
1. Introduction
The Pythagoras theorem is one of the most known results in mathematics and also one of the oldest known. There are hundreds of demonstrations of this theorem. The understanding of the theorem is easy and has numerous applications in real life, as we will see in exercises in this section. It also has uses in advanced mathematics as well (vectorial analysis, functional analysis...)
2. The Theorem
Given a right triangle with sides a and b and a hypotenuse h (the side opposite the right angle). Then,
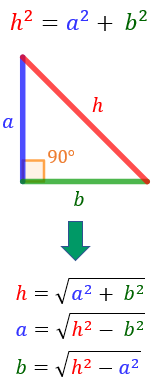
Remember that...
Remember that...
- triangle is a right-angled triangle because it has a right angle, an angle of 90º or π / 2 radians
- the hypotenuse is the opposite side as the right angle.
3. Applying the Pythagoras Theorem
Problem 1: Calculate the hypotenuse of the triangle with sides of 3cm and 4 cm.
Solution:
The sides are and .
Applying the Pythagoras Theorem,
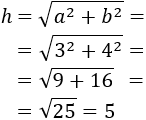
Therefor, the hypotenuse measures 5cm.
Problem 2: If the hypotenuse of a triangle measures 2 cm and one of it's sides measures 1cm, What does the other side measure?
Solution:
We call the sides a and b, and the hypotenuse h.
We know that and .
Because of Pythagoras we know that
Substituting the values we know we have the following equation
Now we isolate b from the equation:
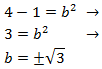
We have written the positive and negative sign because in theory it's what we must do. But because b represents a measurement, it can't be a negative number.
Therefor, the side measures
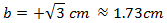
We can leave the square root or reduce it.
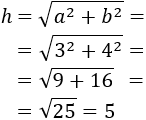
Therefor, the hypotenuse measures 5cm.
Problem 2: If the hypotenuse of a triangle measures 2 cm and one of it's sides measures 1cm, What does the other side measure?
Solution:
We call the sides a and b, and the hypotenuse h.
We know that and .
Because of Pythagoras we know that
Substituting the values we know we have the following equation
Now we isolate b from the equation:
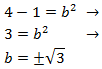
We have written the positive and negative sign because in theory it's what we must do. But because b represents a measurement, it can't be a negative number.
Therefor, the side measures
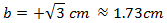
We can leave the square root or reduce it.