Sinus und Kosinus am Einheitskreis (Wel)
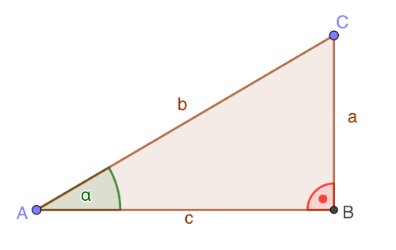
Definition von Sinus, Kosinus und Tangens als Seitenverhältnis im rechtwinkligen Dreieck.
Kreuze alle richtigen Antworten an.
Zur Erinnerung:
und =
Bei der Definition im rechtwinkligen Dreieck ist α beschränkt auf Werte zwischen 0° und 90°.
Um auch andere Winkelwerte verwenden zu können, ist man auf Betrachtungen am Einheitskreis übergegangen.Was ist ein Einheitskreis?
Sinus und Kosinus am Einheitskreis
Man betrachtet nun einen Einheitskreis, dessen Mittelpunkt der Koordinatenursprung ist.
Zugleich ist der Mittelpunkt der Scheitelpunkt des Winkels . Der erste Schenkel ist die positive (!) x-Achse.
Der zweite Schenkel von schneidet dann den Einheitskreis in einem Punkt A.
Die x-Koordinate von A entspricht dann dem Kosinuswert und die y-Koordinate von A dem Sinuswert des Winkels .
Im nächsten Schritt erweitert man auf beliebige Winkel, indem man definiert, dass der Sinuswert eines Winkels weiterhin die y-Koordinate des Schnittpunkts vom 2. Schenkel mit dem Einheitskreis ist und der Kosinuswert die x-Koordinate des Schnittpunkts.
Im nächsten Schritt erweitert man auf beliebige Winkel, indem man definiert, dass der Sinuswert eines Winkels weiterhin die y-Koordinate des Schnittpunkts vom 2. Schenkel mit dem Einheitskreis ist und der Kosinuswert die x-Koordinate des Schnittpunkts.
Bewege den Punkt P und beobachte die Größe beiden Koordinaten.
Wertebereich
In welchem Zahlenbereich liegen die Sinus- und die Kosinuswerte?
Ein kleines Spiel!
Winkel mit gleichen Sinuswerten:
Gesucht wird der Winkel aus dem Intervall (0°, 360°], der den gleichen Sinuswert wie hat.
Tipp: Symmetrie ausnutzen ;)
Frage 1:
= 32° Der Winkel hat den gleichen Sinuswert wie der Winkel . Wie groß ist ?
Frage 2:
= 32° Der Winkel hat nun den gleichen Kosinuswert wie der Winkel . Wie groß ist ?
Frage 3:
= 210° Der Winkel hat den gleichen Sinuswert wie der Winkel . Wie groß ist β? Tipp: Obiges GeoGebra-Applet ist evtl. hilfreich.
Gleiche Kosinuswerte
Entsprechend gibt es zwischen 0° und 360° jeweils zwei Winkel mit dem gleichen Kosinuswert.
Das folgende GeoGebra-Applet veranschaulicht das.
Um beide Winkel zu finden, nutzt man die Symmetrie zur x-Achse aus.