Aplicaciones geométricas
Entre las aplicaciones geométricas de la derivada, tenemos:
- Recta tangente y normal
- Dirección de la curva
- Longitud de la subtangente y subnormal
- Ángulo entre las curvas
Recta Tangente y Normal
La recta tangente a una curva en un punto es aquella recta que pasa por el punto (a, f(a)) y cuya pendiente es igual a .
La recta normal a una curva en un punto es aquella recta que pasa por el punto (a, f(a)) y cuya pendiente es igual a .
Dirección de la curva
La dirección de la curva corresponde al ángulo de separación entre el eje x positivo y la tangente a un punto en la curva, viene dado por:
Longitud de la subtangente y la subnormal
Subtangente. Corresponde a la longitud de la proyección de la tangente sobre el eje x.
Subnormal. Corresponde a la longitud de la proyección de la normal sobre el eje x.
Aplicaciones Geométricas
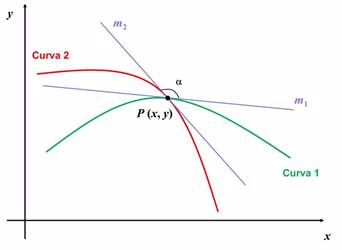
Ángulo entre dos funciones
Para encontrar el ángulo de separación de dos funciones que se intersectan en un punto, se procede a utilizar la misma ecuación aprendida antes, con la diferencia que las pendientes corresponden a las derivadas evaluadas en el punto:
Para encontrar el ángulo:- Encuentre el punto de intersección de las funciones.
- Obtén el valor de las pendientes (derivadas) en el punto de intersección.
- Reemplaza las pendientes en la ecuación.
- Obtén el ángulo de separación.