Multilineare Regression (maschine learning vs normal equation)
3D regression modell of 2 variables
3D visualisation of data with 2 columns dtHead indexed by XAx (xAxis), YAx (yAxis) to last column zAxis.
E(x,y)=(w(1), w(2), w(3)) (x, y, 1)
https://aegis4048.github.io/mutiple_linear_regression_and_visualization_in_python#fig-3
Python Script 4 pyggb
run pyggb: https://www.geogebra.org/python/
code see Question-Tab if link fails
train(X,YY,m= [[0], [0], [0], [0], [0], [0], [0]] iterations= 5000000 lr= 0.0001
Iteration 0 => Loss: 19565836.127127945423126
Iteration 5000000 => Loss: 39323.501278882067709
Weights: [[230.171257789284, 116.37065537484919, -365.0874874857592, 24.97399887846611, -78.58939461161026, 785.1770474081719, -1226.658025934929]]
Normalengleichung (X^T X)^-1 X^T Y
Weights: [[230.29581021003162, 116.22803340440532, -363.73608556960244, 24.996669799201186, -77.4367424162865, 783.1874134816826, -1230.2620369443466]]
A few predictions:
X[0]= -> 4627.0768 (Y label: 4165.2)
X[1]= -> 3417.1248 (Y label: 3561.1)
X[2]= -> 4720.8583 (Y label: 4284.3)
X[3]= -> 5051.8985 (Y label: 5098.7)
X[4]= -> 3822.4808 (Y label: 3406.1)
Machine Learning Supervised Training pyggb
Simple example of supervised learning linear regression
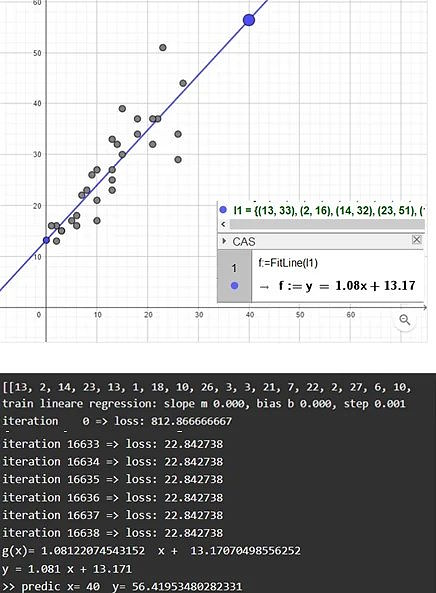
Python Code aegis4048