Limita a spojitost
Limita funkce je nástroj k popisu chování nějaké funkce v okolí určitého bodu. Je-li funkce spojitá, je limita rovna přímo funkční hodnotě. Zajímavé to začíná být právě tam, kde funkce spojitá není, nebo v místech, ve kterých není vůbec definovaná. Pomocí limity můžeme elegantně popsat i kudy funkce míří do nekonečna, tj. zda má nějaké asymptoty.
Příkazy pro určení limit
Limitu v daném bodě můžete určit přímým nástrojem GeoGebry
Limita(f,x0),
ve WolframAlpha Limit[1/x, x -> 0].Definice spojitosti a limity funkce
Říkáme, že funkce f je v bodě x0 spojitá, jestliže ke každému ε>0 existuje δ > 0 takové, že pro každé
x ∈ (a − δ, a + δ) ∩ Df platí nerovnost:
f (x) − f (a) <ε.
Říkáme, že funkce f má ve vlastním bodě x0 limitu A, jestliže pro každé okolí čísla A existuje okolí bodu x0 takové, že je-li
Skok f(x) v bodech x = –2 a x = 2
Posuvníkem x0 zkoumáte spojitost funkce v bodě x0.
K libovolné šířce zeleného pásu eps musíte nalézt modrý pás delta, aby funkční hodnoty všech jeho bodů patřily i do pásu zeleného. Pokud se to nepovede, je funkce v bodě x0 nespojitá.
Řešený příklad
Určete limitu funkce v bodech nespojitosti a v nevlastních bodech ∞,– ∞.
Body x = 1 a x = – 1 nepatří do definičního oboru, funkce zde není spojitá.
Bod x = 1 je tzv. odstranitelnou nespojitostí, protože ať se blížíme k bodu zleva nebo zprava, dostáváme stejnou limitu funkčních hodnot.
.
V bodě x = –1 má hyperbola vertikální asymptotu, limita zleva je – ∞, blížíme-li se k x = –1 zprava, utíkají funkční hodnoty do ∞.
Definice spojitosti pomocí limity.
Literatura
- Vizualizace definice spojitosti v bodě od M. Vinklera.
- Limita funkce a Spojitost na serveru Matematika polopatě (Mathweb)
- Khan Academy: Úvod do limit
- Isibalo: Úvod do limity funkce
Úlohy k procvičení
Určete v bodech nespojitosti limitu funkce a) b)
Úlohy k procvičení:
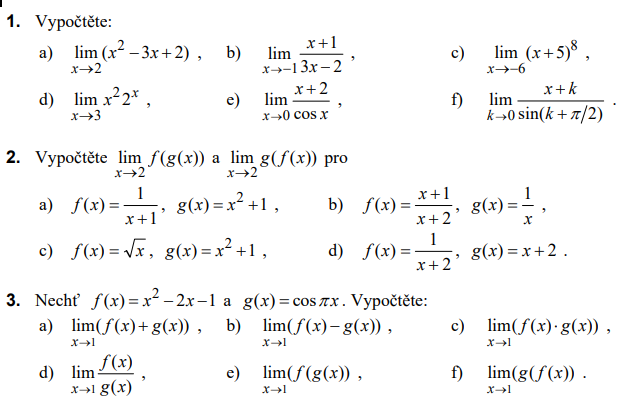
Řešení 1:
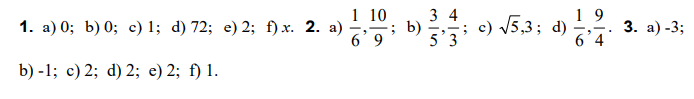
Úlohy k procvičení 2
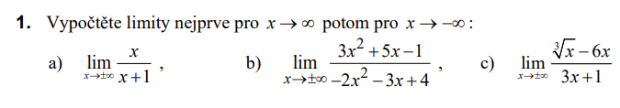
Řešení 2: