Outline
SketchPad Project 1
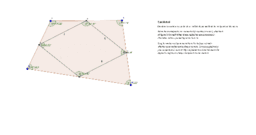
1. Construct an arbitrary quadrilateral in Sketchpad and find the midpoints of its sides.
a. When these midpoints are connected (in clockwise order), what kind of figure is formed? (1pt)
When these midpoints are connected in clockwise order, a parallelogram is formed.
b. Drag the vertices of your quadrilateral to help you decide whether your conjecture is always correct. Can you explain why your conjecture is correct? (1pt)
My conjecture is correct because the opposite angles are always congruent to one another.
2. In a triangle, an altitude is a line segment from a vertex perpendicular to the opposite side. Construct an arbitrary right triangle, acute triangle, and an obtuse triangle in Sketchpad and construct the three altitudes of each triangle.
a. What do you observe about these segments? (1pt)
All of these line segments constructed by the altitudes of the triangles have one point of intersection.
b. What happens for acute triangles, right triangles, and obtuse triangles? (3pts)
• For an arbitrary right triangle, the orthocenter (the intersection of the altitudes) is at the vertex of the 90-degree angle.
• For an arbitrary acute triangle, the orthocenter is closest to the shortest side of the triangle.
• For an arbitrary obtuse angle, the orthocenter is outside of the triangle, behind the obtuse angle.
3. In a triangle, a median is a line segment from a vertex to the midpoint of the opposite side. Construct an arbitrary right triangle, acute triangle, and an obtuse triangle in Sketchpad and construct the three medians of each triangle.
a. What do you observe about these segments? (1pt)
All of the segments that connect the midpoint of a side to an opposite vertex have exactly one point of intersection.
b. What happens for acute triangles, right triangles, and obtuse triangles? (3pts)
For any arbitrary acute triangles, right triangles, and obtuse triangles, the point of intersection for the median is approximately in the middle of the triangle. Unlike the orthocenter, where the point of intersection was not always on the inside of the triangle.