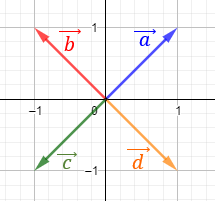
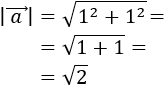Módulo de un vector de R²
Propiedades
Las propiedades básicas del módulo son las siguientes:
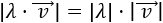
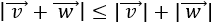 Las demostraciones se encuentran en los problemas 13, 14 y 15 de la página Vectores del plano.
Problemas resueltos de vectores:
Las demostraciones se encuentran en los problemas 13, 14 y 15 de la página Vectores del plano.
Problemas resueltos de vectores:
- El módulo de un vector es siempre mayor o igual que 0, siendo 0 sólo cuando el vector es nulo, es decir, v = (0,0).
- Si λ es un número real, entonces
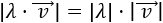
- Dados dos vectores, el módulo de su suma cumple
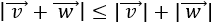 Las demostraciones se encuentran en los problemas 13, 14 y 15 de la página Vectores del plano.
Problemas resueltos de vectores:
Las demostraciones se encuentran en los problemas 13, 14 y 15 de la página Vectores del plano.
Problemas resueltos de vectores:
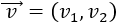 Se define su módulo como
Se define su módulo como
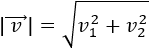
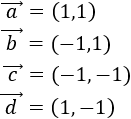 El módulo del primer vector es
El módulo del primer vector es