Volumen Paralelepípedo
Introducción
Mediante esta actividad se pretende facilitar al alumnado la comprensión de un concepto que, a veces, resulta difícil afrontar. Se trata de que el volumen de un paralelepípedo puede obtenerse como producto mixto de tres vectores. Esos vectores son aquellos que confluyen en uno de sus vértices, teniendo cada uno de ellos la longitud de las aristas.
Antes de llegar al concepto último, veamos cómo esos vectores que antes decíamos efectivamente dan lugar a un paralelepípedo. En el primer applet puede observarse como, a partir de tres vectores que se han resaltado en morado, se construye un paralelepípedo. Mueve la figura para comprobarlo debidamente.
A continuación, te toca a ti manejar GeoGebra y hacer una construcción similar a la vista en el apartado anterior. En el applet siguiente, dibuja tres vectores cualesquiera y, posteriormente, ayudándote de la herramienta que permite dibujar vectores equipolentes a unos dados, construye un paralelepípedo. Una advertencia he de hacerte al respecto: sería muy aconsejable que introdujeras los vectores u, v y w a partir de sus coordenadas y no haciendo clic sobre el applet de GeoGebra. Si escoges unas coordenadas adecuadas para ellos, no te costará obtener a ti mism@ el volumen de ese poliedro con lápiz y papel, estando así más convencido de que lo que hace GeoGebra, efectivamente, es correcto.
Antes de seguir adelante queremos aprovechar para afianzar un concepto importante que cumple el paralelepípedo como poliedro que es. Se trata del célebre "Teorema de Euler" que dice lo siguiente:
Dados:
 = Número de caras
= Número de caras
 = Número de vértices
= Número de vértices
 = Número de aristas
de un poliedro convexo, siempre se cumple entre ellos la siguiente relación:
= Número de aristas
de un poliedro convexo, siempre se cumple entre ellos la siguiente relación:

 = Número de caras
= Número de caras
 = Número de vértices
= Número de vértices
 = Número de aristas
de un poliedro convexo, siempre se cumple entre ellos la siguiente relación:
= Número de aristas
de un poliedro convexo, siempre se cumple entre ellos la siguiente relación:

Obtén para nuestro paralelepípedo los valores de C, V y A y comprueba si cumple, o no, el Teorema de Euler:
Un paralelepípedo tiene:
Con los datos de partida anteriores, ¿se cumple el Teorema de Euler?
A continuación, como ya tenemos claro que tres vectores en el espacio forman un paralelepípedo, enlacemos con el propósito de demostrar que el producto mixto de esos vectores es igual al volumen de la figura que dichos vectores generan (debemos decir más exactamente que es igual en valor absoluto, puesto que puede suceder que salga del mismo valor pero con signo negativo).
Un vídeo del canal de YouTube "Mates con Andrés" servirá como introducción teórica:
Vídeo de Mates con Andrés sobre el producto mixto de tres vectores
Vuelve al applet de GeoGebra donde creaste el paralelepípedo y calcula el volumen de dicha figura. Para ello deberás ayudarte del comando "Prisma" que construirás señalando los cuatro vértices de la base del mismo y uno de los vértices de la base opuesta. En la imagen que te tienes a continuación puede ver a qué me refiero:
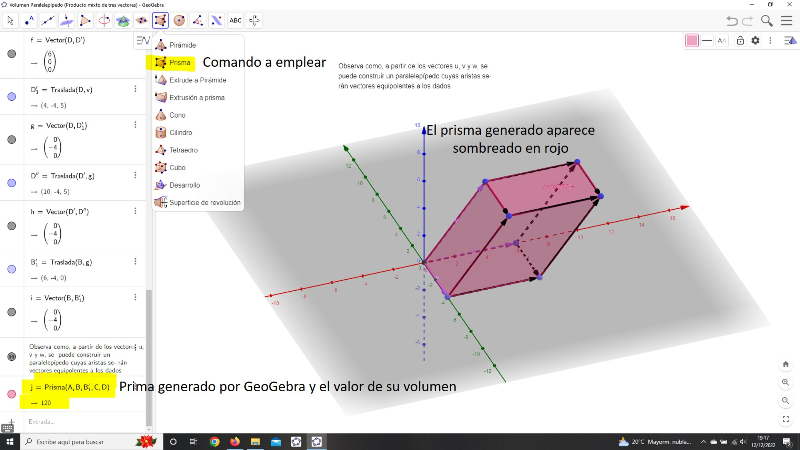
Una vez que hayas generado el prisma y tengas su volumen llegamos al punto clave de estos apuntes que es comprobar que dicho volumen puede obtenerse como producto mixto de los tres vectores que dan lugar a dicho paralelepípedo.
Esto lo vas a hacer en el mismo applet que has utilizado anteriormente y quiero que calcules el producto mixto de dos formas diferentes:
- Mediante la definición de producto mixto, es decir, haciendo: donde · designa producto escalar y designa producto vectorial de los vectores v & w.
- Mediante el determinante formado con las componentes de los tres vectores, que es como lo obtiene Andrés en su vídeo.
Una vez comprendido y asimilado que, efectivamente, el volumen de un paralelepípedo puede obtenerse de la forma expuesta, os presento a continuación unos applets relacionados con esta actividad porque me parece que complementan bien el trabajo hecho a lo largo de la misma.
El primero de ellos es uno que hice yo mismo hace algún tiempo en el que trazo, a partir de un paralelepípedo, tres pirámides que constituyen la mitad de dicha figura. Este hecho se puede comprobar viendo cuánto suman los volúmenes de las tres pirámides.
El siguiente es uno de Javier Cayetano y por último otro de una chica que se hace llamar Vicky en Recursos de GeoGebra. El de Javier Cayetano busca que puedas visualizar cómo un prisma de base triangular (que representa la mitad de un paralelepípedo), puede descomponerse en tres pirámides de base triangular, hecho que permite hallar el volumen de una pirámide como 1/6 del volumen del prisma correspondiente. El de Vicky obtiene los volúmenes de pirámide y paralelepípedo, corroborando que siempre se encuentran en relación 1:6. Con ello completamos la utilidad del producto mixto pudiéndolo extender a las figuras anteriores de forma que el volumen del prisma de base triangular sería 1/2 del volumen del paralelepípedo mientras que el de la pirámide sería 1/6 del mismo
Applet de Julián A. Durán Maestre
Y hasta aquí esta actividad que espero te haya sido de ayuda para aprender que se puede calcular volúmenes con la ayuda del álgebra.