Images. n=24: Biscribed Snub Cube (laevo) and n=32. Their Dual Polyhedrons
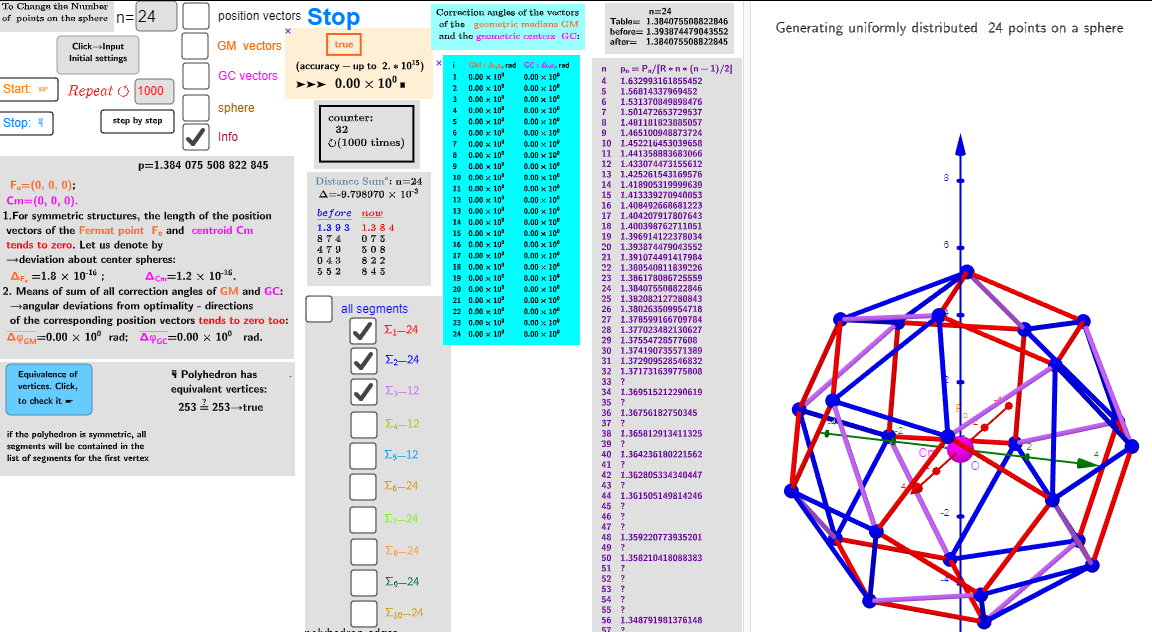
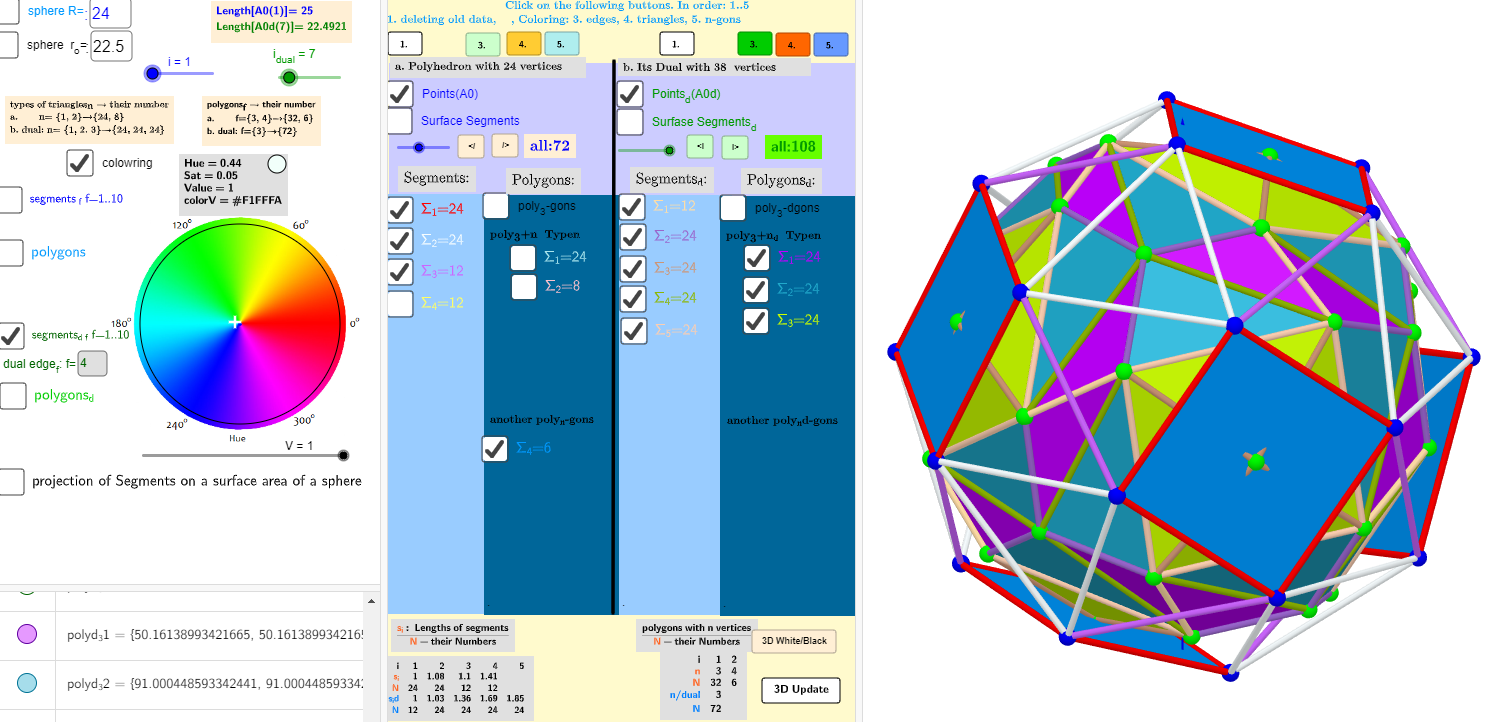
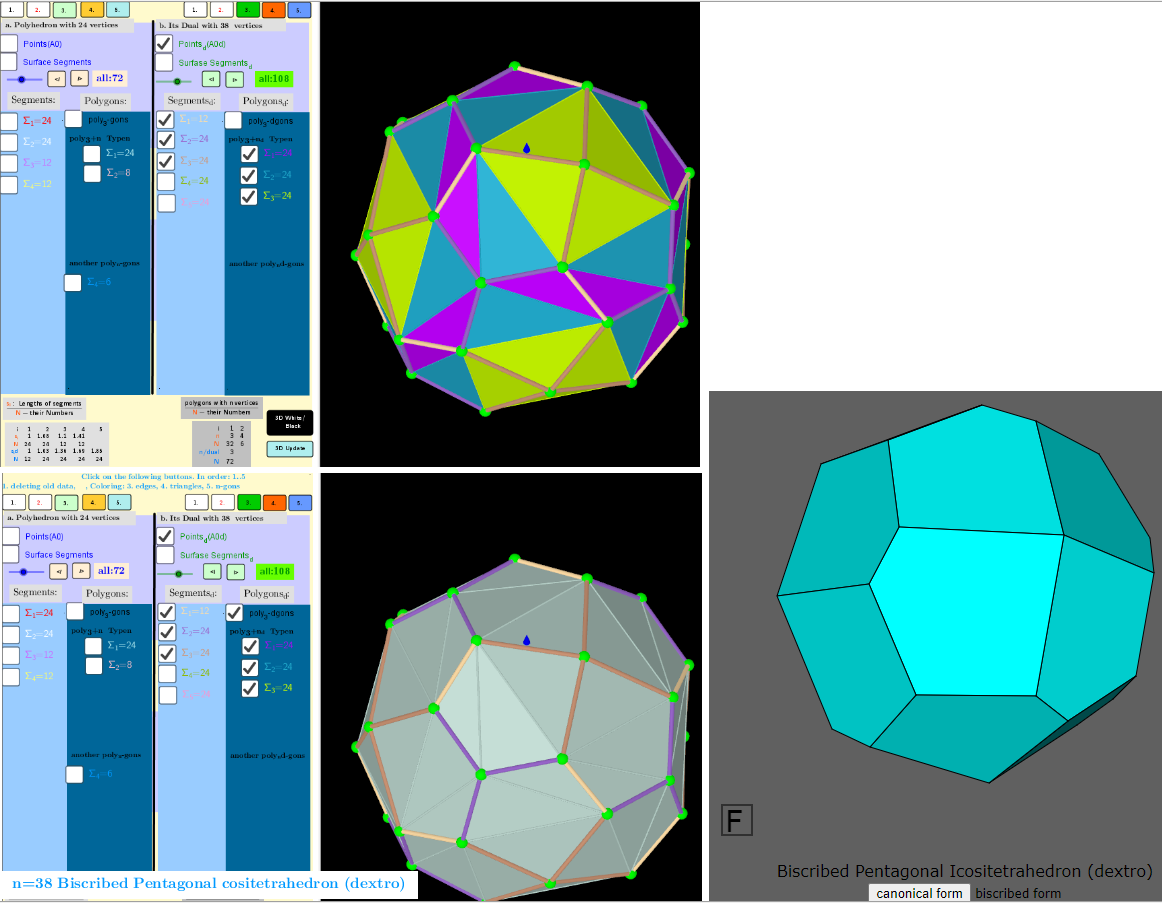
n=24; Biscribed Snub Cube (laevo)
Vertices: 24 (24[5])
Faces: 38 (8 equilateral triangles + 24 acute triangles + 6 squares)
Edges: 60 (24 short + 24 medium + 12 long)
→n=38; Dual Solid: Biscribed Pentagonal Icositetrahedron (dextro) biscribed form
Vertices: 38 (32[3] + 6[4])
Faces: 24 (irregular pentagons)
Edges: 60 (12 short + 24 medium + 24 long)

Comparison of dual polyhedra
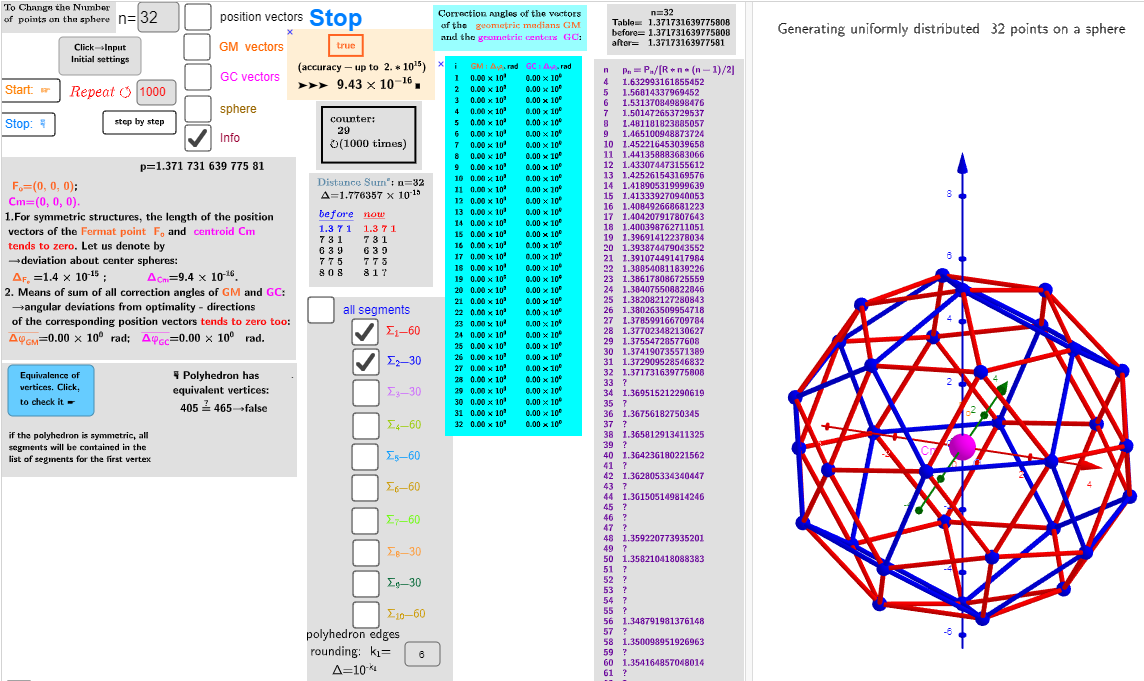
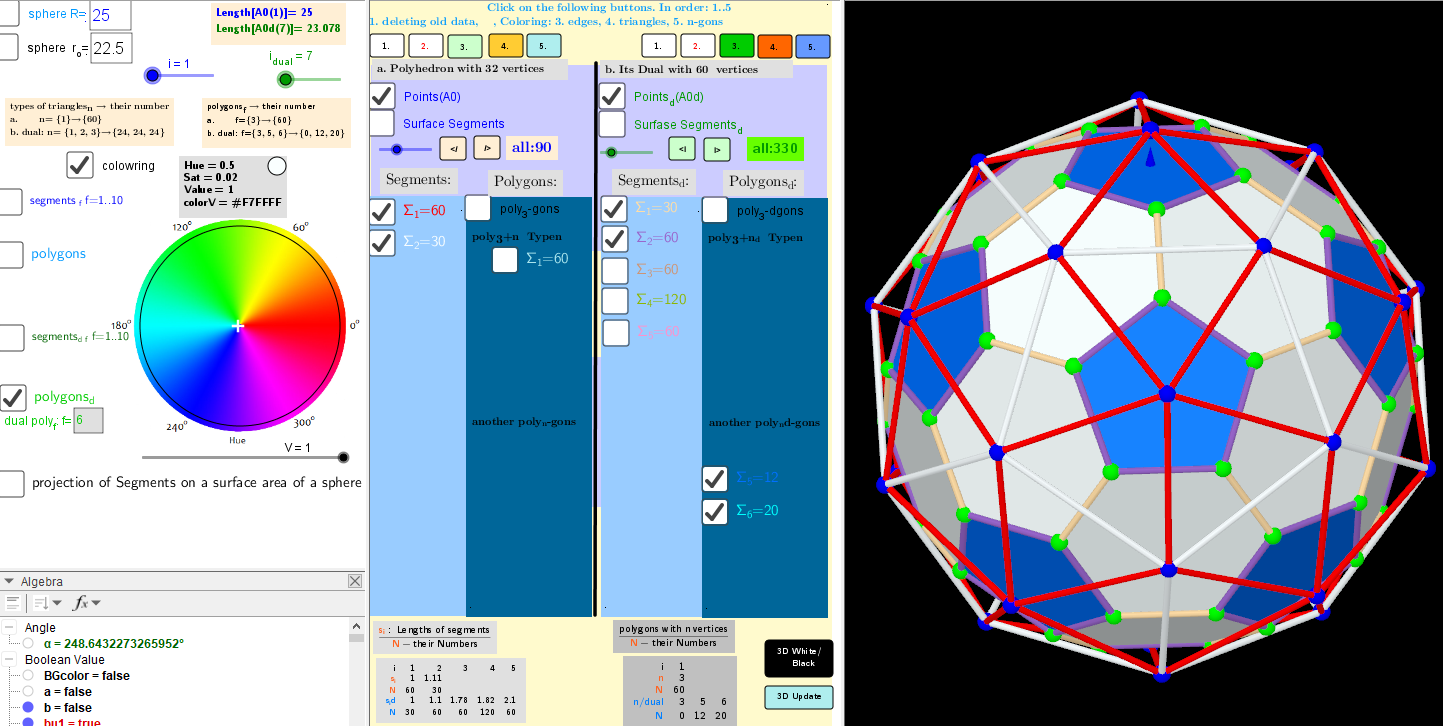
n=32; Biscribed Pentakis Dodecahedron
→ dual: n=60; Biscribed Truncated Icosahedron
| Vertices: | 32 (12[5] + 20[6]) |
| Faces: | 60 (isosceles triangles) |
| Edges: | 90 (60 short + 30 long) |
| Vertices: | 60 (60[3]) |
| Faces: | 32 (12 regular pentagons + 20 ditrigons) |
| Edges: | 90 (30 short + 60 long) |