Kohärenz
Mit freundlicher Genehmigung von Michael Rode.
Wenn man über Kohärenz klassisch denkt, kommt man in erhebliche Schwierigkeiten, sobald man Experimente mit einzelnen Photonen durchdenkt.
Darstellungen, wie sie z.B. bei Pohl zu finden sind, geraten an ihre Grenzen, weil über Interferenz ja für jedes einzelne Photon abgerechnet wird durch Zeigerketten, die man jeder denkbaren Verbindung Quelle- Detektor zuschreibt.
- Die Wellengruppen müssen sich trotz ihrer begrenzten Länge im Beobachtungsgebiet überlappen oder durchschneiden. Die eine Wellengruppe dar den Beobachtungsort nicht vor oder nach der anderen passieren.
- Bei Wiederholungen dieses Vorgangs muss zwischen dem Eintreffen der ersten und der zweiten Wellengruppe stets die gleiche Zeit verstreichen. Andernfalls wechselt das Interferenzbild von Mal zu Mal seine Geschalt. Aus Pohl, R.W.: Optik
Schwieriger wird es, wenn man sich mit Kohärenz in Interferometern auseinander setzt. Aus diesen Anordnungen stammt der Begriff der Kohärenzlänge. Man kann ihn im Bild einzelner Photonen sicher nicht als Länge eines Wellenzuges interpretieren. Eine angemessene Darstellung kann man sich am Beispiel de Michelson- Interferometers mit einem dynamischen Modell erarbeiten.
Aus einer Quelle werden Photonen einstellbarer Wellenlänge emittiert. Als Grundeinstellung wird Lambda = 632 nm gewählt.
Diese Photonen durchlaufen ein Michelson-Interferometer und werden in einem Detektor registriert.
Der Spiegel SR ist zunächst auf den Wert 5 cm eingestellt, also gleich lange Arme des Interferometers. Verändern kann man die Lage von SR mit dem Schieberegler Lage RS, der in Einheiten von 600 nm eingerichtet ist.
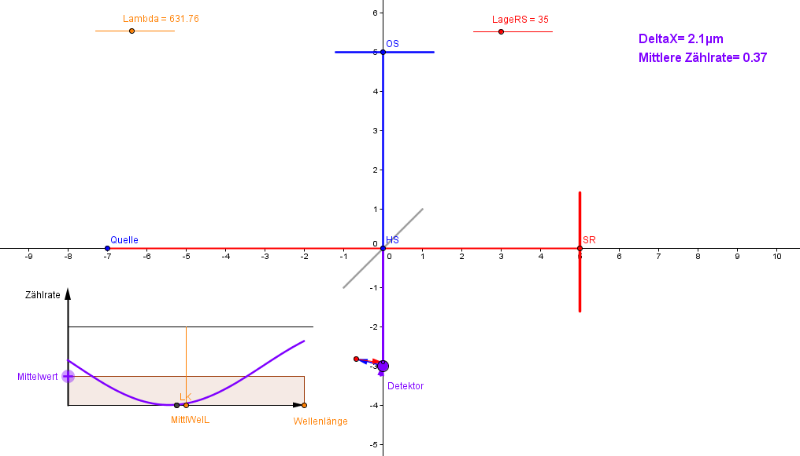
Man erkennt, dass eine schwankende Wellenlänge im Fall gleich langer Arme nicht zu schwankender Intensität führt. Das Diagramm unten links stellt nämlich die gemessene Intensität über der Wellenlänge dar. Die Fläche unter dem Diagramm stellt den Mittelwert aller Nachweiswahrscheinlichkeiten dar. Im vorliegenden Fall ist dieser Mittelwert 1
Jetzt wird SR auf einen anderen Wert eingestellt, am besten so, dass am Detektor für die mittlere Wellenlänge von 632 nm ein Minimum angezeigt wird.
Die anschließende Veränderung der Wellenlänge mit dem Schieberegler zeigt, dass der Kontrast der angezeigten Intensität geringer wird.
Durch Bewegen des Mittelwertes mit der Maus kann man die mittlere Nachweiswahrscheinlichkeit bestimmen, indem man nach Augenmaß die Flächen über dem Mittelwert gleich groß mit denen unter der Kurve macht.
Bei zu großen Abständen zu SR wird man bei voller Variation der Wellenlänge sogar eine Schwankung der Intensität zwischen Null und dem Maximalwert erhalten. Dann wäre Interferenz nicht mehr nachzuweisen, in diesem Fall ist der Abstand zwischen NormallageSR und SR größer als die Kohärenzlänge der Strahlung.
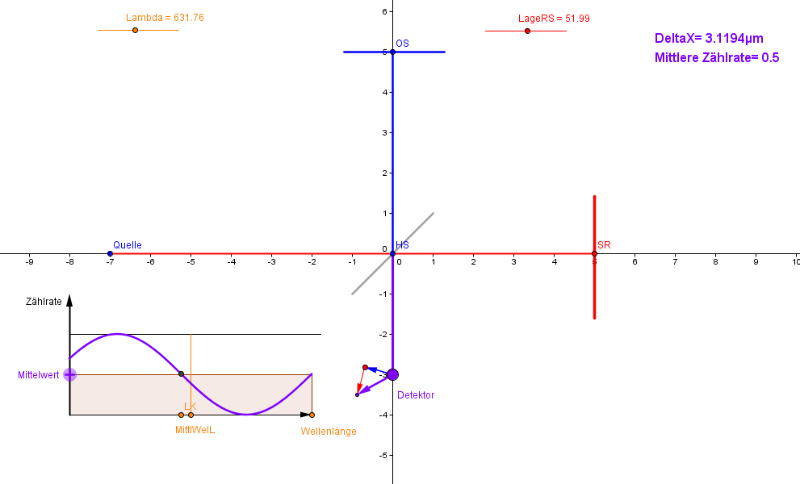
Dann ist die Nachweiswahrscheinlichkeit für ein Photon an diesem Ausgang des Interferometers 0,5. Man kann also Interferenz nicht mehr nachweisen.
Ein „in Massenveranstaltung“ gewonnenes Interferenzmuster wird unter dieser Bedingung völlig verschwimmen - das bedeutet, dass das benutzte Licht nicht mehr kohärent ist.
Nehmen wir an, dass ein Laser die Frequenz 1015 Hz und die Bandbreite 1GHz=10^9Hz besitzt. Dann wird nach 0,5*106 Wellenlängen ein Minimum von einem Maximum überdeckt werden. Das ist bei rotem Licht etwa nach 0,5 m der Fall - nicht wegen der Länge irgendwelcher Wellenzüge sondern wegen der schwankenden Wellenlänge des Lichtes. Es wird dabei nochmals darauf hingewiesen, dass Kohärenz bei einzelnen Photonen ein leerer Begriff ist und erst in der Massenveranstaltung hervortritt.
