Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Teil 3: Bremsweg eines Autos

Autor:Alina Lutzke

Die folgenden Faktoren können den Bremsweg eines Autos beeinflussen:

  • Wetter und Fahrbahnoberfläche (z.B. nass, trocken, ...)
  • Reaktionszeit
  • Beschaffenheit der Reifen
  • Qualität der Bremsanlage
Wir haben in unserem GeoGebra-Applet diese Faktoren außen vor gelassen und die vereinfachte Bremswegformel verwendet. Es wird also nur der Zeitpunkt ab dem Betätigen der Bremse bis hin zum Stillstand des Autos betrachtet. Den Reaktionsweg lassen wir erst einmal außen vor. Hanna und Jonas wollen sich jetzt auf die Suche nach einer Funktionsgleichung für den Bremsweg machen, doch dafür wollen sie erst einmal herausfinden, welcher funktionale Zusammenhang zwischen Bremsweg und der Geschwindigkeit besteht. Denn wie ihr sicherlich herausgefunden habt, liegt hier kein linearer Zusammenhang vor! Zum einen haben lineare Funktionen eine Gerade als Graph. Dies liegt bei unserem Geschwindigkeit-Bremsweg Graph nicht vor, da dieser eher bogenförmig ist, meint Hanna. Zum anderen ist die Steigung bei linearen Funktionen immer gleich. Bei unserem hier vorliegenden funktionalen Zusammenhang ist die Steigung an jeder Stelle unterschiedlich. Die Kerzen aus unserem Experiment sind also in einem bestimmten Zeitabschnitt immer um die selbe Höhe abgebrannt. Wie ihr schon herausgefunden habt, verdoppelt sich der Bremsweg aber nicht, wenn die Geschwindigkeit verdoppelt wird, sondern vervierfacht sich.

Aufgabe 11

Jonas findet in den Unterlagen seiner Schwester folgende Aussage: "Die Länge des Bremsweges kannst du grob abschätzen, indem du die Zahl, die die Geschwindigkeitsanzeige des Autos angibt (in km/h), durch zehn teilst und danach quadrierst." Könnt ihr hiermit auf die Formel des Bremsweges kommen? Notiert die Formel!

Aufgabe 12

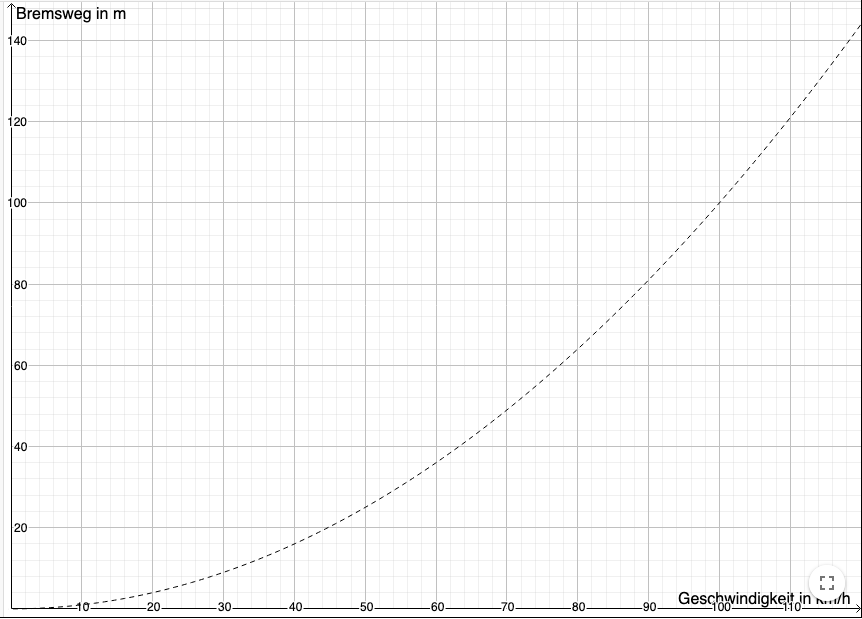
Berechnet mit der Formel aus Aufgabe 11 den Bremsweg für eine beliebige Geschwindigkeit und überprüft euer Ergebnis im Graphen. Liegt der Punkt auf dem Graphen?

Image
Hanna hat mit Hilfe ihres Mathebuches herausgefunden, dass es sich bei ihrem Graphen, um den einer quadratischen Funktion handelt. Graphen von quadratischen Funktionen heißen Parabeln und sind symmetrisch zur y-Achse. Der Graph der Funktion wird Normalparabel genannt.

Hanna hat sich folgendes zur Normalparabel notiert:

Hanna hat sich folgendes zur Normalparabel notiert:

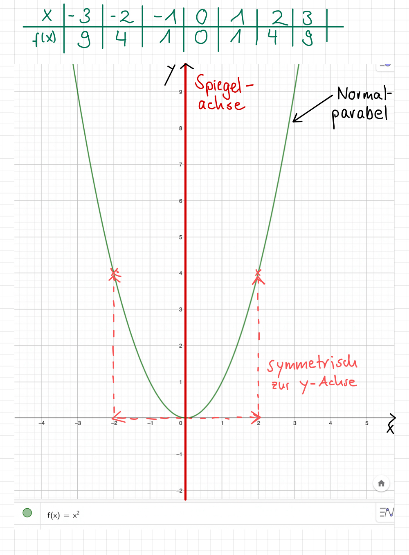
Hanna hat nun selbst ein GeoGebra-Applet erstellt und will die Werte der Normalparabel mit der Funktion vergleichen und damit Eigenschaften des Parameters , herausfinden und so die quadratischen Funktionen entdecken. Helft ihr, die folgenden Fragen zu beantworten.

Aufgabe 13

Wie müsste Parameter gewählt sein, sodass der Graph so aussieht wie der unseres Bremswegs? Schaut euch hierfür die Formel aus Aufgabe 11 nochmal genauer an. Könnt ihr hier eine Verbindung zu der allgemeinen Formel erkennen? Notiert euren Lösungsweg und das Ergebnis.

Klickt im GeoGebra-Applet die Schaltfläche Bremsweg Graph anzeigen an. Stellt den Schieberegler so ein, dass die blaue Funktion genau über der des Bremsweg-Graphen liegt. Überprüft, ob eure Antwort in Aufgabe 13 mit dem Wert in der Simulation übereinstimmt.

Aufgabe 14

An dem eingeblendeten Schieberegegler könnt ihr den Parameter beliebig verändern. Untersucht in der Simulation wie der Parameter die Funktion beeinflusst. Vergleicht den Graphen immer wieder mit der Normalparabel und beantwortet die folgenden Fragen:

  1. Was passiert, wenn größer ist als 1?
  2. Was passiert, wenn negativ ist?
  3. Was passiert, wenn zwischen 0 und 1 liegt?

Sprawdź odpowiedź
Jonas und Hanna fassen ihre Erkenntnisse über quadratische Funktionen noch einmal in einem Merkkasten zusammen. So könnt auch ihr nochmal sehen, was ihr heute zu quadratischen Funktionen alles gelernt habt.
Image

Nowe zasoby

Odkryj zasoby

Odkryj tematy