判別する〜集団の平均点の垂直2等分線
0.問題
<相関比>
2つの集団がまざって分布しているとき、どこに境界線をひくのかという問題が判別問題です。
分散は平均との差の2乗の平均ですが、個数で割る前の2乗和を変動といいます。
平均からの距離の2乗を集団で合計したものです。
集団Pと集団Nのそれぞれの平均をmp, mn,とします。全体の平均をmとします。
全体変動(全変動)はT=Σ(x-m)2、
集団内の変動の和(群内変動)はI=Σ(xp-mp)2+Σ(xnーmn)2
集団の平均どうしの変動和(群間変動)はJ=Σ(m − mp)2+Σ(m - mn)2
T=I+J(全変動=群内変動+群間変動)となります。
TにしめるJの値が大きいと、それぞれの集団のかたまりが強いことになります。
2集団の分離がよりはっきりしています。
相関比=群間変動の比率=J/Tまたは、J/Iの値が判別の強さを表しているともいえます。
<課題1>
男子10人女子10人の身長x、体重yのデータから、男女を判別するx1とx2の関係式をさがす。
| 番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | 151.1 | 155.9 | 159.4 | 154.6 | 162.9 | 158.3 | 171.7 | 160.8 | 153.4 | 161.2 |
| y | 43.7 | 46.2 | 49.5 | 56.3 | 50.9 | 63.5 | 59.8 | 51.7 | 58.3 | 46.8 |
| 性 | F | F | F | F | F | F | F | F | F | F |
| 番号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x | 184.9 | 181.3 | 171.4 | 168.6 | 162.3 | 179.9 | 179.5 | 173.4 | 167.9 | 177.9 |
| y | 75.5 | 78.9 | 66.2 | 61.0 | 55.7 | 80.6 | 66.1 | 61.2 | 61.3 | 77.2 |
| 性 | M | M | M | M | M | M | M | M | M | M |
1.課題1
男子群p、女子群nを判別する直線w1x1+w2x2=bをw={{w1},{w2}},x={{x1},{x2}}と列ベクトルをとると、
法線ベクトルへの正射影の長さがbとなるベクトル方程式wt x=bとなるね。
そのwとbを求めたい。
x=(x1,x2)のデータが原点を通り法線ベクトルを方向ベクトルとする「直線上L」に射影される。
男子xpの平均ベクトルはmp,女子xnの平均ベクトルはmn.
平均ベクトルの直線L上の射影はw' mp, w' mnとなる。'は随伴行列(共役複素数の転置)。
群間J=(w' mp - w' mn)2=(w' (mp- mn))(w'( mp -mn))'=w' (mp-mn)(mp-mn)' w = w' B wとおける。
群内I=Σ(w' mp-w' xp)2+Σ(w' mn- w' xn)2=w' (Σ(mp-xp)(mp-xp)' + Σ(mn-xn)(mn-xn)' ) w=w' W wとおく。
J/I=J(w)= w' B w / w' W w が最大になるwを求めるにはJ(w)のwでの偏微分=0から、
結局、B w =λ W wとなるwとλを求めればよいね。
Wの逆行列をかけると、inv(W)B w =λ w という固有方程式ができる。
だから、行列inv(W)Bの固有値をα、固有ベクトルをwとすると、.......(途中略)。w=inv(W)(mp-mn).
wは2つの群の平均mp、mnの中心を2等分する直線の傾き、つまり、平均の差のベクトルに直交して、
中点を通ればよいのです。正射影の長さbは直線L上での中点だから、b=1/2(w'(mp+mn))
これで判別直線wt x=bと決まるね。
<julia>
using LinearAlgebra
using Statistics
x11=[184.9,181.3,171.4,168.6,162.3,179.9,179.5,173.4,167.9,177.9]
x12=[151.1,155.9,159.4,154.6,162.9,158.3,171.7,160.8,153.4,161.2]
x21=[75.5,78.9,66.2,61.0,55.7,80.6,66.1,61.2,61.3,77.2]
x22=[43.7,46.2,49.5,56.3,50.9,63.5,59.8,51.7,58.3,46.8]
m1=[mean(x11) mean(x21)]
m2=[mean(x12) mean(x22)]
x1=[[x1 x2] for (x1,x2) in zip(x11,x21)]
x2=[[x1 x2] for (x1,x2) in zip(x12,x22)]
mx1=[transpose([m1[1]-p m1[2]-q]) for (p,q) in x1]
mx2=[transpose([m2[1]-p m2[2]-q]) for (p,q) in x2]
s1=sum([[x[1]^2 x[1]*x[2] ;x[1]*x[2] x[2]^2] for x in mx1])
s2=sum([[x[1]^2 x[1]*x[2] ;x[1]*x[2] x[2]^2] for x in mx2])
W=s1+s2
invW=inv(W)
w = normalize(invW *(m1-m2)')
mid=(m1+m2) *0.5
#w[1]x1+w[2]x2-b=0 slope= -w[1]/w[2] y_intersect=b/w[2]
sl=floor(-w[1]*10/w[2])/10
yi= mid[2]+ mid[1]*(-sl)
print("sl=",sl,",yi=",yi)
#========================================================
sl=-3.1,yi=577.662
<julia>
#LDA線形判別分析(Linear Discriminant Analysis)のモジュールを使う。
#Xp,Xnを行列で渡しやすくするためDataFramesモジュールを使う。
w'x+b=0を解くので、bの符号は上記と反対になるので注意。
using LinearAlgebra
using DataFrames
using MultivariateStats
xp=[184.9,181.3,171.4,168.6,162.3,179.9,179.5,173.4,167.9,177.9]
yp=[75.5,78.9,66.2,61.0,55.7,80.6,66.1,61.2,61.3,77.2]
xn=[151.1,155.9,159.4,154.6,162.9,158.3,171.7,160.8,153.4,161.2]
yn=[43.7,46.2,49.5,56.3,50.9,63.5,59.8,51.7,58.3,46.8]
p=DataFrame(datax=xp,datay=yp)
n=DataFrame(datax=xn,datay=yn)
#データをデータフレームから取り出して行列として渡すためにfloat.(Matrix()')でくるむ。
Xp = float.(Matrix(p)');
Xn = float.(Matrix(n)');
f = MultivariateStats.fit(LinearDiscriminant, Xp, Xn);
w=f.w
b=f.b
sl=-w[1]/w[2]
yi=-b/w[2]
print("sl=",sl,",yi=",yi)
#========================================================
sl=-3.022262684795434,yi=564.6938610775744
# PyPlotを使って視覚化する。
using PyPlot
xp=[184.9,181.3,171.4,168.6,162.3,179.9,179.5,173.4,167.9,177.9]
yp=[75.5,78.9,66.2,61.0,55.7,80.6,66.1,61.2,61.3,77.2]
xn=[151.1,155.9,159.4,154.6,162.9,158.3,171.7,160.8,153.4,161.2]
yn=[43.7,46.2,49.5,56.3,50.9,63.5,59.8,51.7,58.3,46.8]
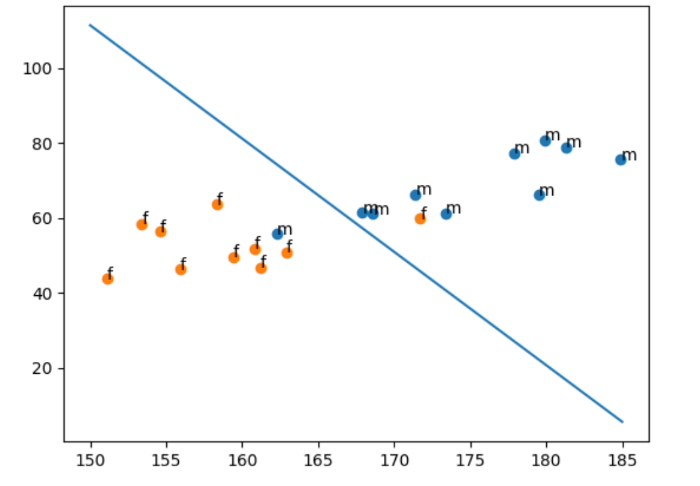
# 男子の点
plt.scatter(xp,yp)
m = ["m","m","m","m","m","m","m","m","m","m"]
for (i, txt) in enumerate(m)
plt.annotate(txt, (xp[i], yp[i]))
end
# 女子の点
plt.scatter(xn,yn)
f = ["f","f","f","f","f","f","f","f","f","f"]
for (i, txt) in enumerate(f)
plt.annotate(txt, (xn[i], yn[i]))
end
# 判別直線
xs=150:185
#+はブロードキャストのため.+にする。
ys=(xs.*sl).+yi
plt.plot(xs,ys)
<Python>
import numpy as np
from statistics import mean
from numpy.linalg import inv,norm
xp=np.array([184.9, 181.3, 171.4, 168.6, 162.3, 179.9, 179.5, 173.4 ,167.9 ,177.9])
yp=np.array([75.5,78.9, 66.2, 61.0, 55.7, 80.6, 66.1 , 61.2, 61.3, 77.2 ])
xn=np.array([151.1, 155.9, 159.4, 154.6, 162.9,158.3,171.7,160.8,153.4,161.2])
yn=np.array([43.7, 46.2, 49.5, 56.3, 50.9, 63.5, 59.8, 51.7, 58.3, 46.8])
mp=np.array([mean(xp) ,mean(yp)])
mn=np.array([mean(xn) ,mean(yn)])
xp=[np.array([x1 ,x2]) for (x1,x2) in zip(xp,yp)]
xn=[np.array([x1 ,x2]) for (x1,x2) in zip(xn,yn)]
mxp=[np.array([mp[0]-p, mp[1]-q]) for (p,q) in xp]
mxn=[np.array([mn[0]-p, mn[1]-q]) for (p,q) in xn]
sp=sum([np.array([[x[0]**2 ,x[0]*x[1]] ,[x[0]*x[1], x[1]**2]]) for x in mxp])
sn=sum([np.array([[x[0]**2 ,x[0]*x[1]] ,[x[0]*x[1], x[1]**2]]) for x in mxn])
W=sp+sn
invW=inv(W)
w = invW @(mp-mn)
w = w/norm(w)
mid=(mp+mn) *0.5
#w[1]x1+w[2]x2-b=0 slope= -w[1]/w[2] y_intersect=b/w[2]
sl=int(-w[0]*10/w[1])/10
yi= mid[1]+ mid[0]*(-sl)
print("sl=",sl,",yi=",yi)
#========================================================
sl= -3.0 ,yi= 560.98