The Orthocenter
Orthocenter
The orthocenter of a triangle is the point of intersection of any two of three altitudes of a triangle (the third altitude must intersect at the same spot). The orthocenter can also be considered as a point of concurrency for the supporting lines of the altitudes of the triangle.
Drawing (Constructing) the Orthocenter
Let's build the orthocenter of the ABC triangle in the next app. 
- The line segment needs to intersect point C and form a right angle (90 degrees) with the "suporting line" of the side AB. Definition of "supporting line: The supporting line of a certain segment is the line
- which contains that segment" The first thing to do is to draw the "supporting line". Enable the tool LINE (Window 3) and click on points A and B. A line d will appear.
- Enable the tool PERPENDICULAR LINE (Window 4), click on vertex C and then click on the supporting line d or on side c¹.
- Select the tool INTERSECT (Window 2). Click on the lines d and e. The point D will be appear.

- The altitude relative to side BC must be drawn now. First, let's draw the supporting line relative to side BC. Enable the tool LINE (Window 3) and click on vertices C and B. A line “f” will appear.
- Enable the tool PERPENDICULAR LINE (Window 4), click on vertex A and then on the line “f” or on side “a”.
- Enable the tool INTERSECT (Window 2), click on line f and then on line g. A vertex E will appear. This vertex is the foot of the altitude relative to side BC. Line g is the supporting line of that altitude.
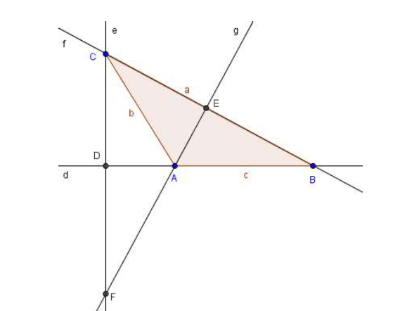
- Now there are two supporting lines to the altitudes, correct? One relative to side AB and the other relative to side BC. Shall we mark where these lines intersect? With the tool INTERSECT TWO OBJECTS (Window 2) still enabled, click on line e (supporting line to the altitude relative to side AB) and on line "g"; (supporting line to the altitude relative to side BC). A new point will appear (point F). This point is the orthocenter of the triangle.
- Enable the tool MOVE GRAPHICS VIEW (Window 11) to adjust the position of the objects in the Viewing Window and use the mouse to adjust the zoom. If all the procedures were followed correctly, you will have a figure similar to the one below.

- The altitude relative to side BC must be drawn now. First, let's draw the supporting line relative to side AC. Enable the tool LINE (Window 3) and click on vertices A and C. A line “h” will appear.
- Enable the tool PERPENDICULAR LINE (Window 4), click on vertex B and then on the line “h” or on side “b”. A line i will appear. Does this line go through the point F (orthocenter)? From this moment point F will be called orthocenter. In order to do this, right click the mouse on vertex F and select the option RENAME. In the new window that appears, type orthocenter and click OK.
Analysis 1
When will the triangle have an internal orthocenter? When will the triangle have an external orthocenter? When will the orthocenter coincide with one of the vertices?
Property
The supporting lines of the altitudes of a triangle intersect at the same point.
Analysis 2
If the orthocenter would lie outside the triangle, would the theorem proof be the same?
Angle formed by altitudes
Analysis 3
Move the vertices of the previous triangle and observe the angle formed by the altitudes. When will this angle be acute? When will this angle be obtuse?