Vektoren_GeoGebra
2D / 3D Koordinatensystem
Bisher kennst du das Koordinatensystem mit 2 Achsen, x- und y- Achse.
Stell dir nun vor, wie noch eine Achse hinzukommt. Diese kommt dir sozusagen entgegen.
Dabei werden die Achsen nun auch anders beschriftet:
= "rote" Achse
= "grüne" Achse = "alte" x- Achse
= "blaue" Achse = "alte" y-Achse
Punkt
Ein Punkt hat die Koordinaten P(x1/x2/x3)
Hier erkennst du den Weg, den man "laufen" muss, um an einen Punkt zu kommen.
Die entsprechende Koordinate nach x1, nach x2 und nach x3 gehen und schon kommst du an dem Punkt an.
Versuche nun die 3 Punkte in dem Koordinatensystem abzulesen.
Die Summe der einzelnen Koordinaten ist die Kontrolle.
A==3
B==5
C==-5
Übung
Mit den Schieberegler kannst du nun alle geforderten Punkte darstellen, so wie oben beschrieben. Du kannst das Koordinatensystem drehen und die Schieberegler richtig einstellen.
AUFGABE:
Stelle die Punkte A-D mithilfe der Schieberegler dar!
Zur Kontrolle kannst du auf den blauen Punkt vor dem Buchstaben klicken.
Wichtig ist nun, dass das mit dem Ablesen auf dem Zettel nicht ganz so einfach ist, wie am Computer. Da kann man schließlich das Koordinatensystem so drehen, dass man alles erkennt. Auf dem Zettel benötigt man jedoch eine Koordinate, von der man ausgeht, damit man den Punkt ablesen kann.
Der Rest funktioniert so, wie am Computer.
Vektoren
Was sind Vektoren? Nun Vektoren sind im allgemeinen eine Menge an Pfeilen, bzw. eine Verschiebung im Raum.
Ein Vektor wird folgendermaßen dargestellt:
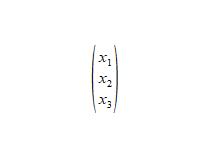
Dir ist sicher aufgefallen, dass die Koordinaten der Achsen () unter einander stehen. Lass dich davon aber nicht irritieren.
Wie bei einen Punkt, wo du im Ursprung startest, kannst du nun von jedem beliebigen Punkt starten und die Verschiebung in wieder als "Weg" ablaufen. Dann nur noch von dem Punkt, wo du gestartet bist, bis zum Endpunkt einen Pfeil und Fertig.
Möchtest du nun einen Punkt als Vektor darstellen, so musst du nur vom Ursprung aus starten und die Koordinaten einzeln "abgehen". Wie beim Punkt. Jetzt nur noch untereinander schreiben.
Zu schnell? Hier nochmal zur Veranschaulichung
Der dünne graue Weg beschreibt die einzelne Koordinaten des Vektors
Du gehst nun von Punkt A -2 Einheiten in x1 Richtung, 3 Einheiten in x2 Richtung und 2 Einheiten in x3 Richtung. Und schon bist du bei Punkt B.
Doch Vektoren sind Ortsunabhängig, dass heißt, sie können ohne Punkt existieren und man kann sie sogar Verschieben. Probiere mal aus, den Vektor zu verschieben, in dem du ihn am Anfang anklickst und mit der Maus verschiebst.
Dass lässt sich besser im 2D- Koordinatensystem machen, aber denk dran, es funktioniert auch in 3D!
Möchtest du nun einen Vektor mithilfe zweier Punkte aufstellen und ausrechnen, ohne den "Weg" abzulaufen, so musst du die Koordinaten des Endpunktes (Spitze) Minus die Koordinaten des Startpunktes (Schaft) rechnen. Im Allgemeinen sieht das so aus:
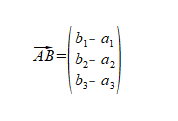
Nehmen wir nun die Koordinaten des Beispieles von oben. Da wissen wir ja schon wie der Vektor auszusehen hat:
![[size=100]Wir sehen, GeoGebra hat richtig gerechnet :)[/size]](https://stage.geogebra.org/resource/nJTXx7Rz/OhMgurKpe0dPqvws/material-nJTXx7Rz.png)
Versuche nun selbst die angegebenen Vektoren mithilfe der Punkte zu bestimmen:
von A zu B, von C zu D und von E zu F