Aplicación del Teorema de Rouché-Frobenius
Recordad que un sistema de ecuaciones lineales (SEL) puede representarse de forma matricial como A·X = b, donde A es la matriz de coeficientes, X es la matriz columna de incógnitas y b es la matriz columna de términos independientes. Recordad que el SEL es
- compatible determinado: si tiene solución y es única.
- compatible indeterminado: si tiene solución no única. En este caso, existen infinitas soluciones.
- incompatible: si no tiene solución.
Teorema de Rouché-Frobenius
"Sea el sistema A·X=b con m ecuaciones lineales y con n incógnitas, donde m y n son naturales mayores que 0. Entonces,
- El sistema A·X = b es compatible si, y sólo si, rango(A) = rango(A|b)
- El sistema A·X = b es compatible determinado si, y sólo si, rango(A) = rango(A|b)= n"
Ejemplo de aplicación
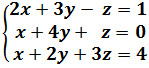
La matriz ampliada del sistema es
La matriz ampliada del sistema es
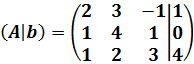 El rango de la matriz es
El rango de la matriz es
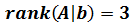
ya que tiene un determinante de dimensión 3 no nulo:
ya que tiene un determinante de dimensión 3 no nulo:
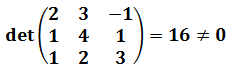
Además, como el determinante anterior también es el determinante de la matriz A, la matriz de coeficientes también tiene rango 3:
Además, como el determinante anterior también es el determinante de la matriz A, la matriz de coeficientes también tiene rango 3:
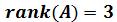
Por tanto, tenemos que los rangos de las dos matrices coinciden
Por tanto, tenemos que los rangos de las dos matrices coinciden
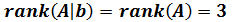
y, por el teorema de Rouché-Frobenius, como el rango es igual al número de incógnitas, el sistema es compatible determinado.
En efecto, la única solución del sistema es, en forma matricial,
y, por el teorema de Rouché-Frobenius, como el rango es igual al número de incógnitas, el sistema es compatible determinado.
En efecto, la única solución del sistema es, en forma matricial,
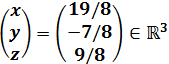
Es decir,
Es decir,
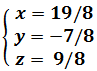 Nota: la solución se ha calculado por la regla de Cramer.
Nota: la solución se ha calculado por la regla de Cramer.