Résolution de l'inéquation 2x+3 <=4
Méthode graphique 1
En considérant (x) = 2x+3 et g(x)=4, résoudre l'inéquation 2x+34 revient à trouver pour quelles valeurs de x, (x) g(x)
(x) est une fonction affine dont la courbe représentative est une droite.
Pour la tracer, on a besoin de deux points :
Si x=0, y = 3
Si x=1, y = 5
Droite d'équation y = 2x+3
Puis on trace la courbe représentative de g(x) =4
C'est une droite horizontale puisque y est constante.
Droites d'équation y = 2x+3 et y=4
Les points vérifiant f(x)g(x) sont les points pour lesquelles la courbe de f (noire) est en dessous de la courbe de g (verte)
Droites d'équation y = 2x+3 et y=4
C'est la partie du plan à gauche de l'intersection des deux droites.
Ce sont donc tous les x inférieurs ou égaux à 1/2
Méthode graphique 2
Résoudre l'inéquation 2x+34 revient à résoudre l'inéquation 2x-10
On peut alors considérer la fonction h(x) = 2x-1 et trouver les points pour lesquels cette fonction est inférieure à 0.
Les solutions de l'inéquation 2x-10 sont les valeurs de x situées à gauche de l'intersection de la droite et de l'axe des abscisses (y=0).
Ce sont donc tous les x inférieurs ou égaux à 1/2
Tracé complet
Remarque : Les droites d'équation y = 2x+3 et y=2x-1 ont meme coefficient directeur (2) et sont donc parallèles
Méthode avec tableau de signes
Résoudre l'inéquation 2x+34 revient à résoudre l'inéquation 2x-10, donc à trouver toutes les valeurs de x pour lesquelles l'expression 2x-1 est inférieure ou égale à 0.
On cherche d'abord les valeurs de x qui annule cette expression.
Ici 2x-1 = 0 x = 1/2
On peut alors écrire le tableau de signes suivant :
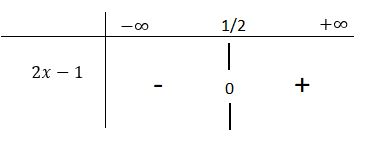
L'inéquation 2x+34 , c'est à dire 2x-1 0 est résolue pour tout x inférieur ou égal à 1/2
Méthode algébrique
On cherche à résoudre 2x+3 4, c'est à dire à trouver les valeurs de x qui vérifient cette inéquation.
2x+34 2x 1 x 1/2
Les solutions de l'inéquation sont tous les x inférieurs à 1/2
C'est la partie du plan à gauche de l'intersection des deux droites.
Ce sont donc tous les x inférieurs ou égaux à 1/2
Quelle méthode choisir?
La méthode graphique est à privilégier lorsque la résolution algébrique est complexe et/ou lorsque le tableau de signes est risque d'erreurs (beaucoup de quotient ou de facteurs)