Dale Copy of Interior Angles of Regular Polygons
We just learned that we can calculate the total number of degrees of interior angles of any polygon by using the formula 180(n - 2). If we know that the polygon is a regular polygon (all sides and angles are congruent) we can take it one step further and calculate the degree measure of each angle of the regular polygon.
Using the slider below, create a regular pentagon (5 sides). To find the total number of degrees for the interior angles you use the formula 180(n - 2). To find one angle of a regular pentagon you use the formula . So you find the total number of degrees and then divide by the number of angles.
1) Create a regular hexagon (6 sides).
What is the total number of degrees for the interior angles? What is the degree measurement of 1 angle of a regular hexagon?
2) Create a regular octagon (8 sides).
What is the total number of degrees for the interior angles? What is the degree measurement of 1 angle of a regular octagon?
3) Solve for x. You must first find the number of degrees in 1 angle of a regular pentagon. Answer below.
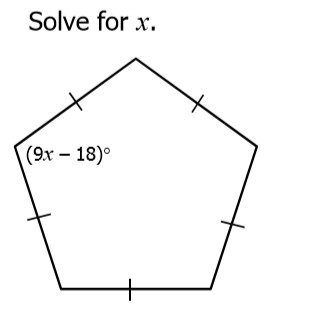
4) Solve for x. You must first find the number of degrees in 1 angle of a regular hexagon. Answer below.
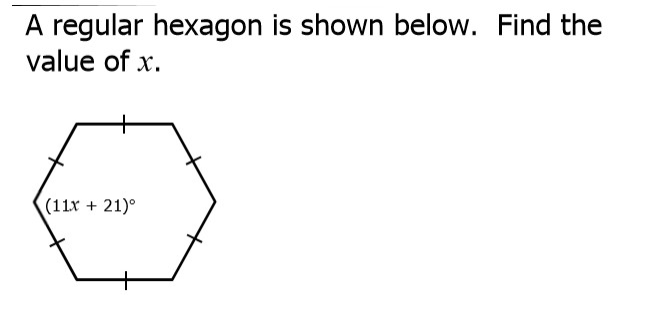
5) Solve for x. You must first find the number of degrees in 1 angle of a regular decagon. Answer below.
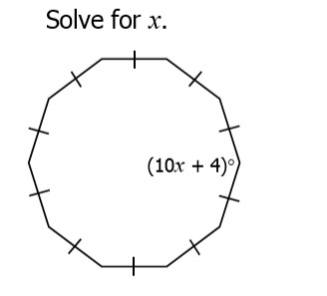
Answers to 3 - 5.
3. 4. 5.