an 'einstein' tile - een 'einstein' tegel...
David Smith discovers an 'einstein'
It took some 50 years after Roger Penrose to surprise the tiling world with an astonishing tile.
While in 1974 Penrose used two different tiles (a kite and a dart) David Smith, a retired hobbyist who likes puzzles, created a hat-shaped tile thet can fill the entire plane in a pattern that never repeats.
A German once called such a tile an "einstein" , referring to the German word "ein Stein" (one stone) and of course also to the genius who eventually would be able to find it.
Smith contacted some academics who confirmed that the hat-tile indeed was aperiodic.
This means you cannot outline a region of the tiling and tile the plane by translating copies of that region without rotating or reflecting.
More, soon after Smith created a turtle-tile, being aperiodic too. In fact researchers found out that both tiles belong to an infinite family, tiling the plane the same way.
More about the sensational discovery you can read on Quantamagazine.
And of couse you cannot sidestep what David Smith himself published on Hedraweb.
the hat-tile dissected
For years mathematicians searching for the holy grail in tiling explored the same track: In tiling one knows that regular tilings can be created out of triangles, quadrilaterals and hexagons. So in their search for aperiodic tilings they explored forbidden symmetries, like the fivefold symmetry of the Penrose tiling.
The great surprise now is that the hat-tile is constructed within a tiling of hexagons.
The edges of the thirteenfold hat-tile are very 'common' points:
- 3 centres of hexagons
- 6 midpoints of sides of hexagons
- 4 edges of hexagons
Tiling with David Smith's hat-tile
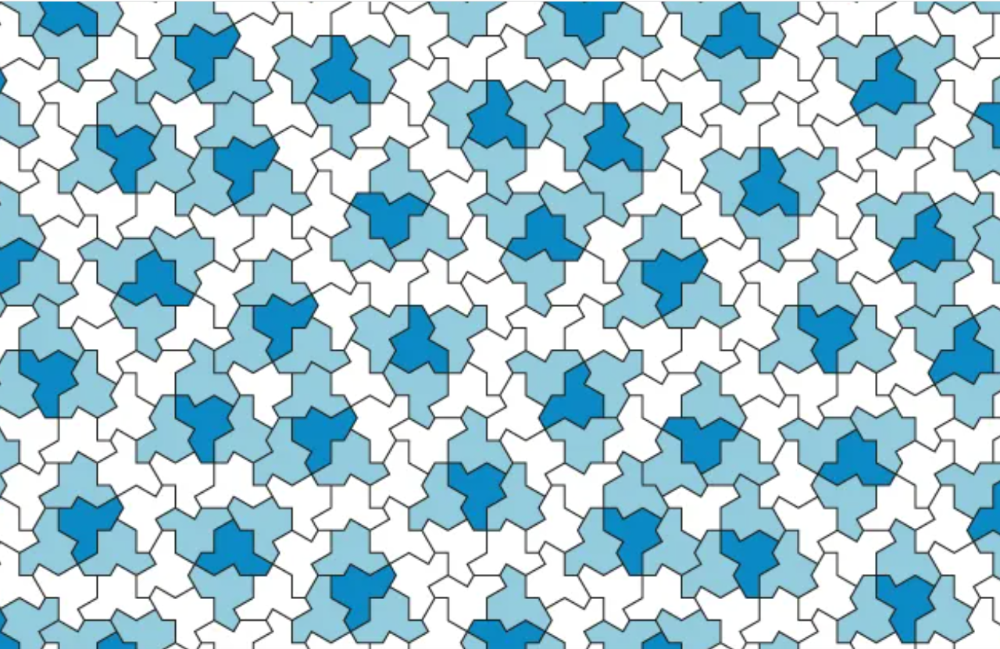
de tegel van David Smith en Penrose betegelingen
Een Nederlandse tekst over de ultieme tegel die Robert Smith creëerde, vind je op de webpagina van het nrc.
Meer over Penrose betegelingen vind je in mijn eerdere Nederlandstalige GeoGebraboek.