SEQUÊNCIA: Intervalos Reais - Introdução
______________________________________________________________________________________________________________________________________________________________ O que é um intervalo real?
______________________________________________________________________________________________________________________________________________________________ Intervalo real, como o nome sugere, é um subconjunto dos números reais (). Esse tema é muito importante para o estudo de funções e seus domínios!Vamos analisar um exemplo abaixo!
A = {x ∊ ℝ / -2 ≤ x < 4}
- Lê-se: x pertence ao conjunto dos números reais tal que -2 é menor ou igual a x e x é menor que 4.
- A expressão x ∊ ℝ significa que o conjunto A é um subconjunto do conjunto dos números reais, ou seja, cada elemento do conjunto A (representado por "x") também pertence ao conjunto ℝ.
- -2 ≤ x < 4 significa que todos os números reais entre -2 e 4 são elementos do conjunto A.
- O número -2 também pertence ao conjunto A. Isso porque -2 ≤ x , ou seja, os elementos do conjunto A são maiores ou iguais a -2. Por haver uma igualdade (maior ou igual a -2). Dizemos que o intervalo é fechado em 2.
- O número 4 não pertence ao conjunto A. Isso porque x < 4, ou seja, os elementos do conjunto A são menores que 4. Qualquer número a esquerda do número 4 (por exemplo, 3,99999) pertence ao conjunto A, mas exatamente o número 4 não pertence. Por não haver igualdade aqui, dizemos que o intervalo é aberto em 4.
Como existem infinitos números reais entre -2 e 4 , existem infinitos elementos no conjunto A. (Veja alguns destaques na figura abaixo)
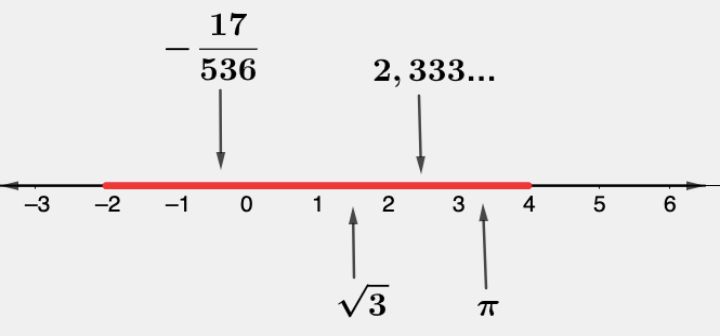
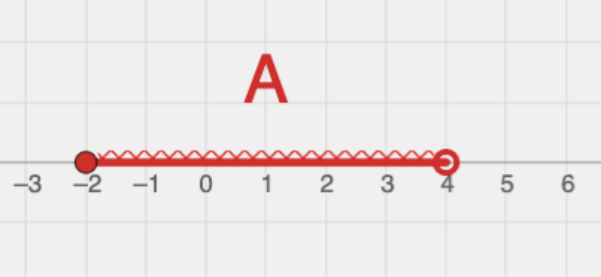
Nessa representação acima podemos perceber que o intervalo A é fechado em -2 (a "bolinha" está fechada -2) e é aberto em 4 (a "bolinha" está aberta em 4). Uma forma muito usada para escrever um intervalo real é o uso de colchetes. A regra é:
- Colchete invertido (ou parênteses) significa que o intervalo é aberto naquela extremidade.
- Colchete em posição normal significa que o intervalo é fechado naquela extremidade.
Veja como podemos escrever o intervalo A:
A = {x ∊ ℝ / -2 ≤ x < 4} ou A = [-2 , 4[ (Lê-se: fechado em -2 e aberto em 4) ou A = [-2, 4) (Lê-se: fechado em -2 e aberto em 4) ______________________________________________________________________________________________________________________________________________________________ Explore o aplicativo abaixo e verifique como escrever intervalos reais! (Para utilizar a tela cheia, clique na figura posicionada no canto inferior direito da tela)
______________________________________________________________________________________________________________________________________________________________
A = {x ∊ ℝ / x ≥ 3}
Nesse caso, o conjunto A possui extremidade à esquerda mas não possui extremidade à direita. Isso significa que não existe um número que seja maior que todos os outros do conjunto A.
Representação:
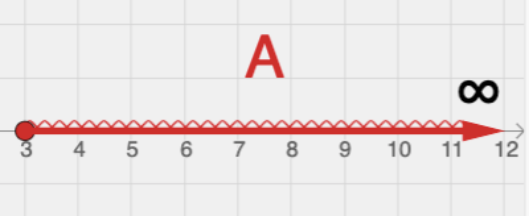
A = [3 , ∞[ ou A = [3 , ∞)
Obs: o símbolo "infinito" sempre é usado com representação de intervalo aberto (colchete invertido ou parênteses). ______________________________________________________________________________________________________________________________________________________________ Agora, observe o conjunto B:B = {x ∊ ℝ / x ≤ 5}
O conceito de infinito também é usado nesse caso, no entanto para a esquerda. Isso significa que não existe um número real que seja menor que todos os outros do conjunto B.
B = ]-∞ , 5] ou B = (-∞ , 5]
Obs: o símbolo infinito à esquerda é usado junto com o sinal negativo. -∞ é lido: "menos infinito". ______________________________________________________________________________________________________________________________________________________________
Olha que interessante!
O intervalo ]-∞ , ∞[ é o próprio conjunto dos números reais ℝ.______________________________________________________________________________________________________________________________________________________________
Explore o aplicativo abaixo e verifique como escrever intervalos reais com extremidades infinitas!(Para utilizar a tela cheia, clique na figura posicionada no canto inferior direito da tela)
Um caso especial ______________________________________________________________________________________________________________________________________________________________
Observe a representação abaixo:
Note que o número 5, não pertence ao intervalo A. Podemos escrever:
A = [1 , 8] - {5} ou ainda A = [1 , 5[ U ]5 , 8]
- O símbolo "- {5}" significa que o número 5 foi retirado do intervalo [1 , 8].
- O símbolo "U" (união) junta os dois intervalos e os chama de intervalo A.