Découvrir l'homothétie
Objectifs de l'activité
Dans cette activité, tu apprendras à construire l'homothétie d'une figure et tu verras ses propriétés.
Voici les tâches que tu auras à faire:
- Consulte le document pour revoir le concept de figures semblables.
- Fais la construction demandée en suivant les étapes. Au besoin, regarde la capsule vidéo.
- Réponds à la question de validation
- Relève le défi pour recréer une figure en utilisant l'homothétie
- Réponds aux questions.
Rappel des propriétés des figures semblables
Instructions pour la construction d'une figure et son image par homothétie
Dans la fenêtre de l'application, construis une figure et son image par homothétie.
- Avec l'outil Polygone
 , trace un polygone dans la fenêtre graphique;
, trace un polygone dans la fenêtre graphique; - Avec l'outil Point
 , place un point à côté du polygone;
, place un point à côté du polygone; - Avec l'outil Curseur
 , place un curseur dans le bas de la fenêtre graphique et nomme-le k; (si le curseur n'est pas dans la liste des outils, clique sur PLUS en bas de la liste).
, place un curseur dans le bas de la fenêtre graphique et nomme-le k; (si le curseur n'est pas dans la liste des outils, clique sur PLUS en bas de la liste). - Sélectionne l'outil Homothétie
 , clique sur la figure, clique ensuite sur le point puis, dans la boite de dialogue, entre la variable k pour le rapport, puis clique sur OK.
, clique sur la figure, clique ensuite sur le point puis, dans la boite de dialogue, entre la variable k pour le rapport, puis clique sur OK. - Reprend l'outil Déplacer
 pour modifier la valeur de k, les sommets de la figure et la position du point. Observe ce qui se passe;
pour modifier la valeur de k, les sommets de la figure et la position du point. Observe ce qui se passe; - Avec l'outil Droite
 , trace une droite qui rejoint les sommets correspondants (par exemple A et A')
, trace une droite qui rejoint les sommets correspondants (par exemple A et A') - Sélectionne l'outil Angle
 et clique dans la figure et dans l'image pour afficher les angles intérieurs.
Si nécessaire, visionne la vidéo sous la fenêtre pour savoir comment faire.
et clique dans la figure et dans l'image pour afficher les angles intérieurs.
Si nécessaire, visionne la vidéo sous la fenêtre pour savoir comment faire.
Construction de l'homothétie
Vrai ou faux: C'est seulement lorsque le rapport d'homothétie égale 1 que les mesures des côtés de la figure initiale et de son image sont les mêmes
Dans l'application suivante, construit une figure semblable et utilise le même rapport d'homothétie
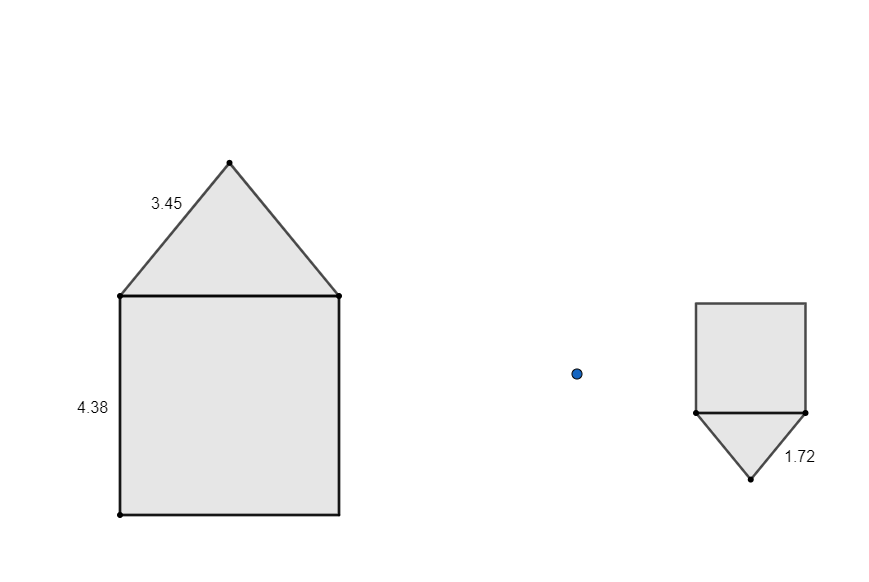
Construction de l'illustration ci-dessus
Dans l'illustration ci-dessus, quelle est la mesure du côté du carré de l'image obtenue par homothétie?
Lorsque l'image obtenue par homothétie est plus petite et à l'envers de la figure initiale, on peut affirmer que:
