Kongruenz von Dreiecken
Heute beschäftigen wir uns damit, was du über ein Dreieck wissen musst, um es eindeutig zu zeichnen.
Wiederholung der bekannten Befehle in Geogebra:
Verschieben von Objekten.
Setzen eines beliebigen Punktes
Markieren des Schnittpunkts zweier Linien
Zeichnen einer Gerade durch zwei Punkte.
Zeichnen eines Kreises mit gegebenem Mittelpunkt sowie einem weiteren Punkt, durch den er geht.
Zeichnen eines Kreises mit gegebenem Mittelpunkt und Radius.
Zeichnen eines Winkels mit festgelegtem Winkelmaß.
Neu dazu kommt heute:
Zeichnen der Strecke zwischen zwei Punkten.
Verschieben von Objekten.
Setzen eines beliebigen Punktes
Markieren des Schnittpunkts zweier Linien
Zeichnen einer Gerade durch zwei Punkte.
Zeichnen eines Kreises mit gegebenem Mittelpunkt sowie einem weiteren Punkt, durch den er geht.
Zeichnen eines Kreises mit gegebenem Mittelpunkt und Radius.
Zeichnen eines Winkels mit festgelegtem Winkelmaß.
Neu dazu kommt heute:
Zeichnen der Strecke zwischen zwei Punkten.Partneraufgabe
Bearbeitet die folgende Aufgabe getrennt voneinander. Einer von euch arbeitet auf dem Papier, während die andere am Tablet arbeitet. Vergleicht danach eure Ergebnisse miteinander.
Konstruiere ein Dreieck mit a = 5 Längeneinheiten und b = 4 LE.
(Bei dieser und allen folgenden Aufgaben ist es kein Problem, wenn die Objekte in Geogebra anders heißen.)
Unter dem Applet gibt es ein paar Hilfestellungen, wenn du Probleme hast. Versuche es aber erst einmal selbst!
Tipps
Die Dreiecke, die du und deine Partnerin konstruiert haben, sahen nicht unbedingt gleicht aus. Beschreibe kurz, woran das liegt.
Partneraufgabe
Probieren wir das ganze noch einmal, diesmal mit mehr Informationen zu dem Dreieck. Tausche dafür mit deinem Partner. Derjenige, der vorher das Tablet hatte, arbeitet nun auf dem Papier und umgekehrt.
Konstruiere ein Dreieck mit den Seitenlängen a = 5 LE, b = 4 LE und c = 6 LE.
Tipps
Vergleiche dein Ergebnis mit dem deiner Partnerin. Beschreibe, was dir auffällt.
Wähle die korrekte Antwort aus und übertrage dann den Hefteintrag in dein Heft.
Ergänze deinen Hefteintrag um die
Konstruktionsanleitung SSS
Bsp: Zeichne ein Dreieck mit den Seitenlängen a = 4 LE, b = 5 LE, c = 2 LE
1. Zeichne eine der Seiten.
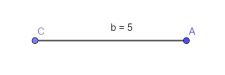
2. Schlage Kreise mit den jeweiligen Seitenlängen als Radius an beiden Endpunkten.
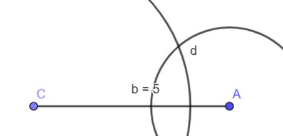
3. Der Schnittpunkt der beiden Kreise ist der 3. Punkt des Dreiecks.
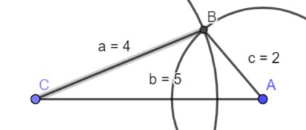
Die Kreise haben aber zwei Schnittpunkte. Erkläre kurz, warum das nicht dazu führt, dass die Konstruktion nicht eindeutig ist.
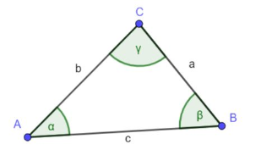
Wdh: Bezeichnungen im Dreieck
Erinnerung: Im Dreieck werden die Eckpunkte, Seiten und Winkel wie hier zu sehen bezeichnet.
Weitere Dreieckskonstruktionen
Bearbeitet nun gemeinsam die folgenden Dreieckskonstruktionen. Wechselt euch am Tablet ab!
(Ihr dürft Winkel abmessen.)
Überprüft bei allen Konstruktionen, ob sie stabil sind, wenn ihr Punkte verschiebt.
1. Konstruiere ein Dreieck mit c = 6 LE, = 30°, = 100°
2. Konstruiere ein Dreieck mit a = 4 LE, c = 6 LE, = 50°.
3. Konstruiere ein Dreieck mit a = 5 LE, c = 3 LE, = 35°
Hefteintrag: Weitere Kongruenzsätze
Zwei Dreiecke sind auch dann kongruent zueinander, wenn sie:
- In einer Seite und den beiden daran angrenzenden Winkeln übereinstimmen (WSW)
- In zwei Seiten und dem eingeschlossenen Winkel übereinstimmen (SWS) oder
- In zwei Seiten und dem an die kürzere Seite angrenzenden zusätzlichen Winkel übereinstimmen (SsW). Übungen Konstruiere abwechselnd in Geogebra und auf dem Papier. Wechsle dich mit deiner Partnerin ab. 1. Konstruiere ein Dreieck mit c = 4 LE, b = 6 LE, = 110°
Konstruiere ein Dreieck mit a = 3 LE, b = 4 LE, c = 5 LE.
3. Konstruiere ein Dreieck mit = = 80°, a = 2 LE
Konstruiere ein Dreieck mit a = 4 LE, b = 6 LE,
Bonus
Konstruiere ein Dreieck mit a = 6 LE, = 50°, = 60°