Grundsätzliche Matrix-Operationen

Autor:hawe

Hinweise

Eine einmal belegte Variable kann von nachfolgendem Code nicht überschrieben/geändert werden - eine Variable ändern heißt erzeuge eine neue Instanz/neue Variable. Ein Matrix-Element kann nicht per Indizes geändert/geschrieben werden sondern man muss eine Zeile Element für Element durchlaufen und eine neue Zeile/Matrix mit der Änderung erzeugen oder Änderungen an (unvollständige) Zeilen anhängen. A := {{11,12,13,14},{21,22,23,24},{31,32,33,34},{41,42,43,44}}

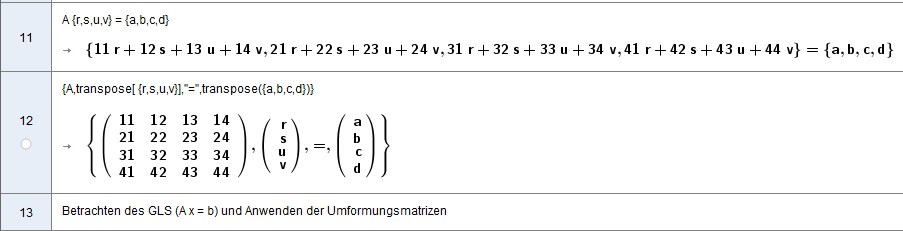
Lineare Gleichungssysteme A

[size=100]Im CAS lege ich eine Matrix A an und verwende Einträge an denen sich leicht die Zeilen und Spalten-Positionen ablesen lassen.
Ich verwende Zahleneinträge, damit sich die Matrixelemente einfach abgreifen lassen:
A(n) steht dann für die Matrixzeile n und A(z,s) steht für das Element in Zeile z, Spalte s![/size] — Im CAS lege ich eine Matrix A an und verwende Einträge an denen sich leicht die Zeilen und Spalten-Positionen ablesen lassen. Ich verwende Zahleneinträge, damit sich die Matrixelemente einfach abgreifen lassen: A(n) steht dann für die Matrixzeile n und A(z,s) steht für das Element in Zeile z, Spalte s!

[size=100]Tauschmatrix zum Vertauschen von Zeilen oder Spalten. Sie entstehen aus der Einheitsmatrix in dem die entsprechenden Zeilen vertauscht wurden: T12, T13, T14, T23, T24, T34 wäre ein kompletter Satz an Matrizen um alle möglichen Zeilen- oder Spalten-Vertauschungen einer 4x4 Matrix zu beschreiben.[/size] — Tauschmatrix zum Vertauschen von Zeilen oder Spalten. Sie entstehen aus der Einheitsmatrix in dem die entsprechenden Zeilen vertauscht wurden: T12, T13, T14, T23, T24, T34 wäre ein kompletter Satz an Matrizen um alle möglichen Zeilen- oder Spalten-Vertauschungen einer 4x4 Matrix zu beschreiben.

[size=100]Anwenden der Tauschmatrix T12 zum Zeilentausch[/size] — Anwenden der Tauschmatrix T12 zum Zeilentausch

[size=100]Anwenden der Tauschmatrix T12 zum Spaltentausch[/size] — Anwenden der Tauschmatrix T12 zum Spaltentausch

[size=100]Inverse: Wende ich eine Tauschmatrix auf sich selber an, dann tausche ich einen Satz vertauschter Zeilen wieder zurück und ich erhalte die Einheitsmatrix.[/size]

[size=150]Umformen von linearen Gleichungssystemen[/size] — Inverse: Wende ich eine Tauschmatrix auf sich selber an, dann tausche ich einen Satz vertauschter Zeilen wieder zurück und ich erhalte die Einheitsmatrix. Umformen von linearen Gleichungssystemen

A x = b Eine Matrix-Gleichung kann einfach von Links mit einer Zeilentauschmatrix multipliziert werden um eine Zeilenoperation in der Matrix A durchzuführen. T12 A x = T12 b Um an der Matrix A eine Spaltenoperation durchzuführen kann die Matrix-Gleichung nicht einfach von rechts multipliziert werden, da die Tauschmatrix dann bei x einen Spaltentausch durchführem will wo keine Spalten sind. A x T12 = b T12 Bringen wir zwischen A x die Einheitsmatrix in Form von zwei Tauschmatrizen T12 T12 = E ein, so tauschen wir in A die Spalten und in x die Zeilen, was dann das GLS erhält - wir haben ja nur mit der Einheitsmatrix E multipliziert.

A x = b

Das GeoGebra-Ergebnis A x = b etwas schöner aufgeschrieben:

Zeilentausch: T12 A x = T12 b

Zeilen- & Spaltentausch: T12 A T12 T12 x = T12 b

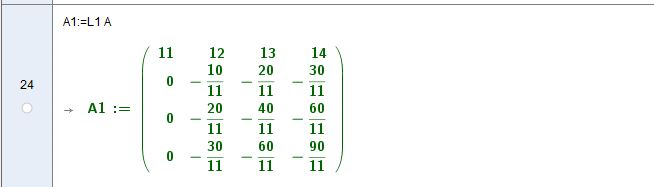
Zeilenumformung zur Lösung eines linearen GLS

Beim Lösen eines GLS mittels Gauss-Algorithmus oder bei der Erzeugung der LR-Zerlegung werden die Zeilen der Matrix A durch Zeilenumformungen auf die Einheitsmatrix oder die Dreiecksmatrizen L R zurückgeführt. Das Standardverfahren addiert ein Faktor q-faches der ersten Zeile zur allen folgenden Zeilen, so dass in der ersten Spalte Nullen entstehen: Die Zeilenumformungsmatrix T2plus1 soll ein q faches der ersten Zeile zur zweiten und ein p-faches der zweiten Zeile zur dritten addieren.

[size=100]Allgemein werden in Zeilentransformationsmatrizen die Faktoren für die erste Zeile unterhalb der Diagonalen in der ersten Spalte und die Faktoren für die zweite Zeile in der zweiten Spalte hinterlegt. Weitere Zeilenfaktoren analog eintragen ...[/size] — Allgemein werden in Zeilentransformationsmatrizen die Faktoren für die erste Zeile unterhalb der Diagonalen in der ersten Spalte und die Faktoren für die zweite Zeile in der zweiten Spalte hinterlegt. Weitere Zeilenfaktoren analog eintragen ...

[size=100]Im Ergebnis erhalten wir Zeile2=q*Zeile1+Zeile2 und Zeile3=p*Zeile2+Zeile3
Die Zeilenumformung Zeile1+Zeile2 soll im Lösungsschritt Gauss/LR-Zerlegung in der ersten Spalte 0 ergeben:
11q + 21 = 0
q = -21/11 oder allgemein q = -A(2,1)/A(1,1)[/size]
Je nach Versionszustand muss die Matrixindizierung auch via Befehl ELEMENT erfolgen: A(2,1) = ELEMENT(A,2,1)! — Im Ergebnis erhalten wir Zeile2=q*Zeile1+Zeile2 und Zeile3=p*Zeile2+Zeile3 Die Zeilenumformung Zeile1+Zeile2 soll im Lösungsschritt Gauss/LR-Zerlegung in der ersten Spalte 0 ergeben: 11q + 21 = 0 q = -21/11 oder allgemein q = -A(2,1)/A(1,1) Je nach Versionszustand muss die Matrixindizierung auch via Befehl ELEMENT erfolgen: A(2,1) = ELEMENT(A,2,1)!

Inverse

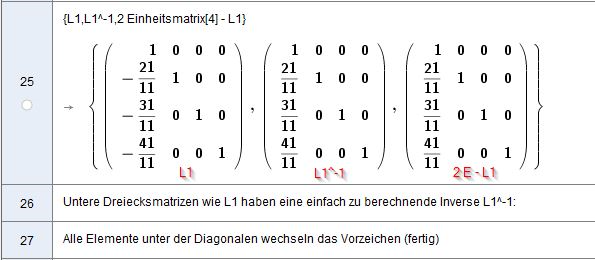
Gauß-Algorithmus R4x4

Aus einer Matrix

generiere ich die Gaußelimationsfaktoren für L₁ aus der 1. Spalte

dividiere durch a₁₁, alle Faktoren mal (-1) (alles unter a₁₁) und fülle zur Einheitsmatix auf. In der 1. Spalte stehen die Faktoren mit denen die 1.Zeile multipliziert wird. Um dann per Matrixprodukt zur Faktorzeile addiert zu werden. Alle Zeilen 2,3,4..n werden geändert mit Nullen in der ersten Spalte.

Wiederhole Algorithmus auf der Matrix (c_ij)

Wiederhole Algorithmus auf Matric (u_ij)

Zusammenfassung

In den diskutierten Beispielen habe ich einige Matrix-Operationen und Eigenschaften der verwendeten Matrizen zusammen gestellt, die auf dem Weg zur Lösung von linearen GLS zur Anwendung kommen. Matrizentechnisch ist ggb schwach aufgestellt. Viele Funktionalitäten fehlen! Zeilenzugriffe {Take(A,2,2),Element(A,2)}

Take => Zeilenvektor, Element => Liste Spaltenzugriffe (transponieren um Spalten als Zeilen abzugreifen und Rücktransponieren zu Spalten) {Transpose(Take(Transpose(A),2,2)),Transpose(Element(Transpose(A),2))}

Uneinheitliches Ergebnis, durchs Transponeren wird die (Element) Liste zum Spaltenvektor? Achtung: Beim Übergang zu LGS n>3 erfolgt auch ein Paradigmenwechsel von Vektor zu Liste/Matrix. Grundsätzlich ist die bisher praktizierte Praxis einen Vektor als Liste {1,2,3,4} darzustellen u.U. ein Problem. Besser ist es einen Vektor als 1-spaltige Matrix zu schreiben {{1},{2},{3},{4}} oder als 1-zeilige Matrix {{1,2,3,4}} die transponiert Transpose({{1,2,3,4}}) wieder eine 1-spaltige Matrix darstellt - macht halt mehr Scheibarbeit. Nach meiner Erfahrung ist das Matrix*Vektor-Produkt (ggb-Vektoren) auch immer für Überraschungen gut - unterscheide Punkt/Vektor!

Ich beginne eine neues Arbeitsblatt um ein konkretes GLS mittels Gauss-Algorithmus bzw. mittels LR-Zerlegung zu lösen. Siehe KonvertGLS2Matrix.ggb, um aus einem in x1,x2,x3... gegebenen GLS die Matrixgleichung A x = b heraus zu ziehen.

Anwendung CAS-User-Functions Lineare Gleichungsysteme

Rang, Kern in-,sur-,bijektiv

Rang der Matrix = Anzahl der Spalten ⇔ Abbildungs-Matrix ist injektiv. Rang der Matrix = Anzahl der Zeilen ⇔ Abbildungs-Matrix ist surjektiv. Kern der Matrix = 0 ⇔ Abbildungs-Matrix ist injektiv. Bei quadratischen Abbildungs-Matrizen folgt aus der Surjketivität die Injektivitiät und umgekehrt aus der Injektivität die Surjektivität. Wenn die Determinante einer quadratischen Matrix ≠0 ist, kann man die Matrix invertieren, also gibt es eine Umkehrabbildung. Die Abbildungs-Matrix ist dann bijektiv. Das gilt auch umgekehrt.