Poliedros con buracos
A fórmula de Euler asegura que un poliedro convexo cumpre sempre que:
Así, que sucede se un poliedro é concavo? Cumpre ou non cumpre a fórmula de Euler? Existe algún poliedro que non a cumpra?
A resposta é que a fórmula é válida para aqueles poliedros que poden "inflarse" até converterse nunha esfera.
DEMOSTRACIÓN DA FÓRMULA DE EULER
Para probar a fórmula procédese por inducción partindo da esfera.
- Ao engadir unha única aresta que sae e chega a un mesmo vértice, tense que , e por tanto cúmprese que .
- Se se engade outro vértice sobre unha aresta xa existente, haberá un vértice máis e a aresta queda dividida en dúas. Co cal, o número de arestas aumenta en un, mentres que o número de caras non se ve alterado.
Así, por cada vértice novo hai un vértice e unha aresta máis; por tanto a conta permanece igual.
- Se se engade unha nova aresta entre dous vértices xa existentes, haberá unha aresta máis que divide a cara en dúas. Co cal, o número de caras aumenta en un, mentres que o número de vértices non se ve alterado.
Así, por cada aresta nova hai unha aresta e unha cara máis; por tanto a conta permanece igual.
En calquera caso, a fórmula sempre é certa porque con estes pasos podemos recrear calquera división da esfera en caras mediante vértices e arestas.
POLIEDROS CON BURACOS
Por tanto, que debe ocorrer para que esa fórmula NON sexa válida? Pois que o poliedro debe ter algún buraco. Nese caso a conta de sofre unha "perda". Vexamos o porqué.
Ao facer un buraco nunha cara, o resultado NON é un polígono, así que xa non podemos contala coma unha soa cara senón que temos que considerar que é a unión de varias.
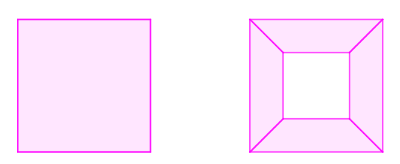
Vemos na imaxe da esquerda que a cara sen buracos cumpre que , é dicir que "aporta" 1 na conta de .
(ollo, non "aporta" o 2 da fórmula porque na imaxe só consideramos un polígono, para termos un poliedro habería que "pechalo")
Unha vez feito o buraco e reconsiderándo a figura como unión de varios polígonos, na imaxe da dereita vese que o reconto é . É dicir, na conta de "perdeuse" 1.
Como no poliedro cada buraco afecta a dúas caras, unha de entrada e outra de saída, con cada buraco que se fai no poliedro "pérdense" 2 na conta total. E de aí que a fórmula para un poliedro con buracos adopte este outro aspecto:
A miña gratitude a Javier Cayetano Rodríguez, pois desta súa aplicación saquei a idea.