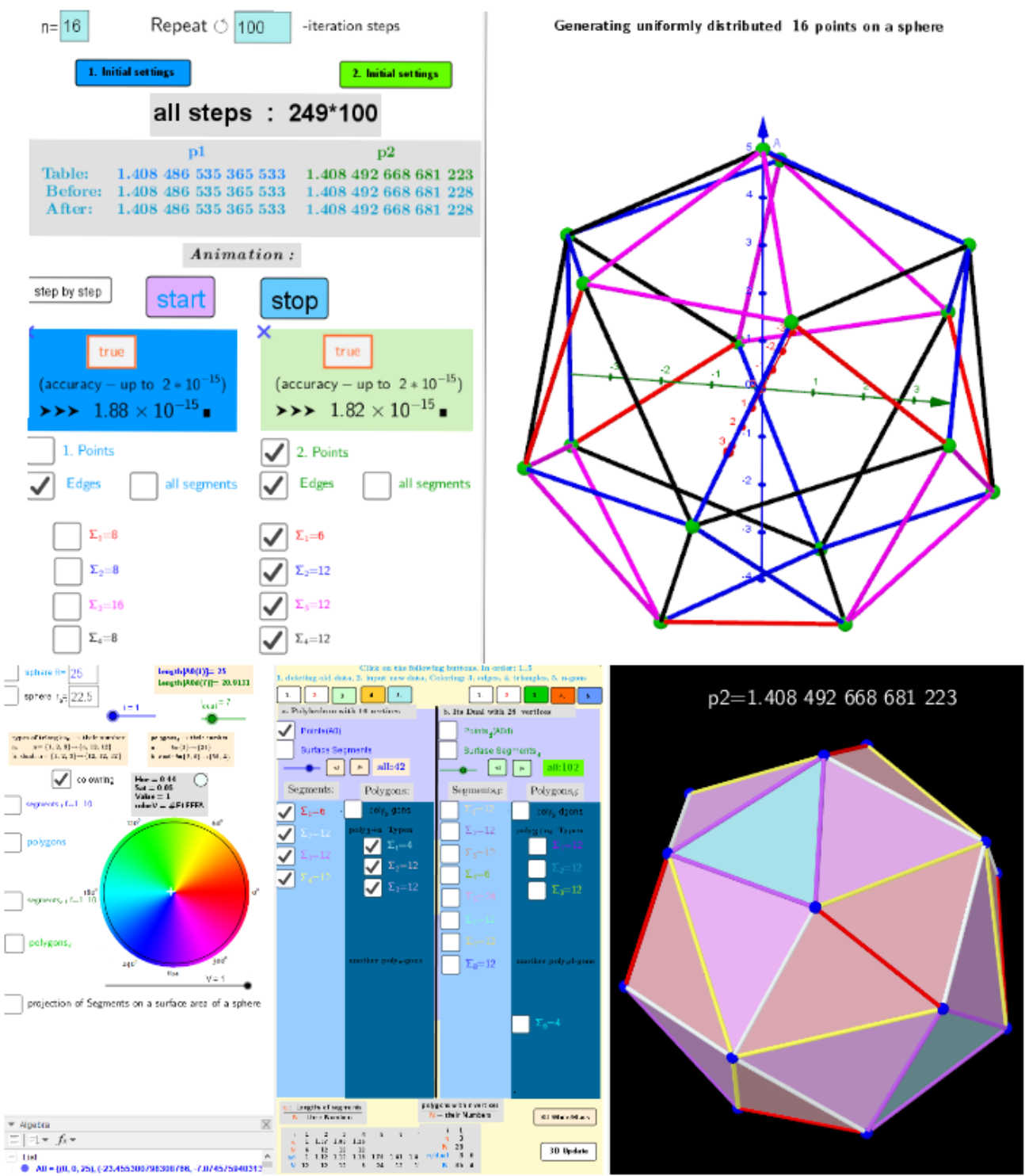
Example of non-uniqueness of the extreme distribution of n=16 particles on the surface of a sphere.
The number of particles on the surface of the sphere is the same. They are placed according to the maximum Distance Sum principle. The "measure" of this distribution is the p-average distance between these particles on the unit sphere. Here, using the example n=16, it is shown, that there are at least two such extreme distributions:
p1 = 1.408 486 535 365 533; p2 = 1.408 492 668 681 228.
These two distributions are obtained here by a different choice of initial settings-distributions for a further iterative procedure.
Images: Variant 1
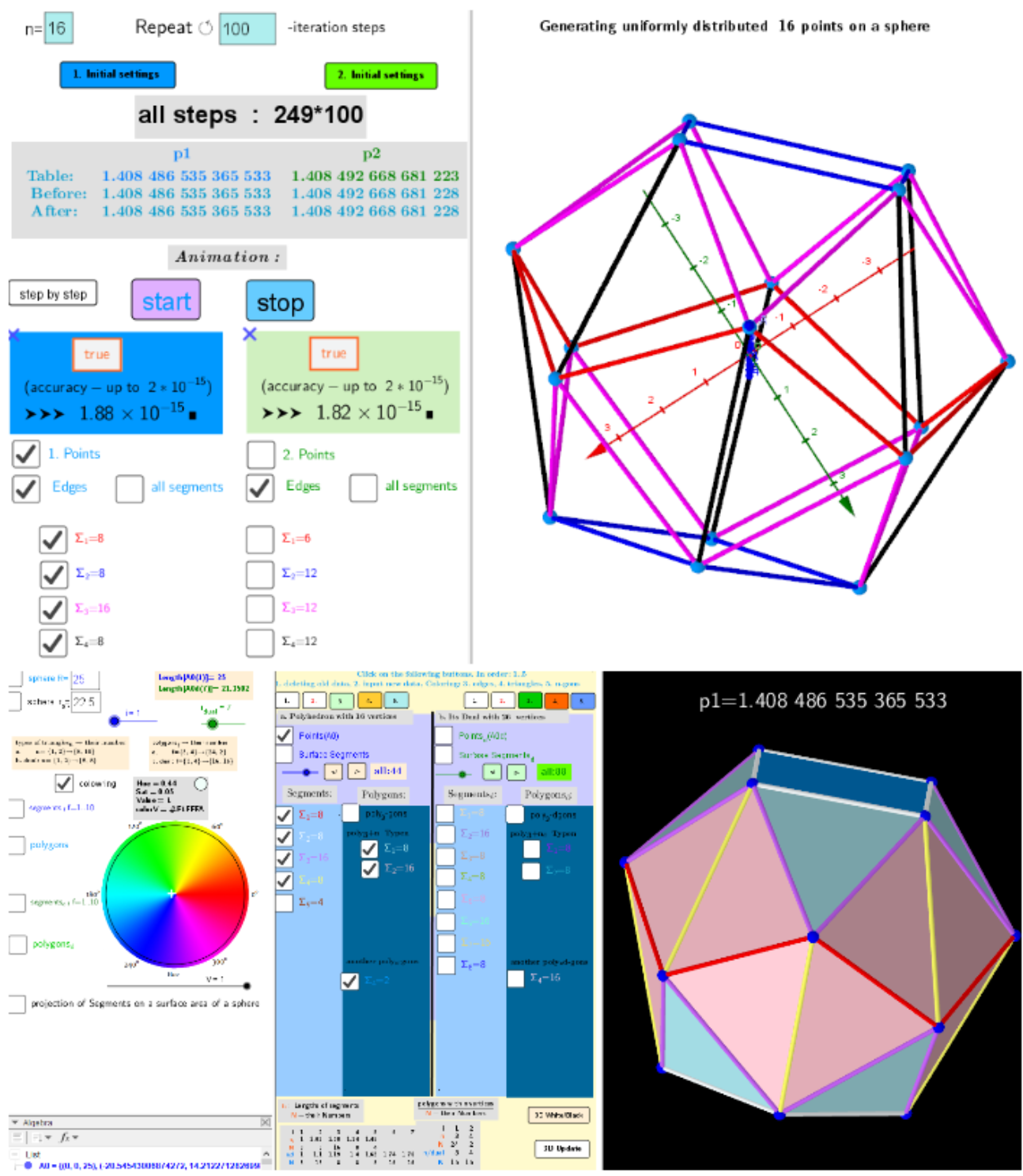
Images: Variant 2