Eén stemming voor 24 toonaarden
Wanneer we spreken over het spelen in verschillende toonaarden, kunnen we niet om Johann Sebastian Bach heen. Hij componeerde in 1722 een reeks van preludes en fuga's in elk van de 24 mogelijke toonaarden "ter gebruik door en ten bate van leergierige jongeren en als tijdverdrijf voor de geoefende muzikant". Twintig jaar later, in 1742, schreef hij nog een tweede bundel. De twee bundels kennen we nu samen als één werk.
'Welgetemperd' betekent dat er geen intervallenvoorkomen die absoluut moeten vermeden worden. Op die manier werd het effectief mogelijk in elke mogelijke toonaard te spelen.
Er is al veel geschreven over de stemming die Bach zelf hiervoor gebruikte. Vast staat dat Welgetemperd niet hetzelfde is als de gelijkzwevende stemming die wij gebruiken. Gelijkzwevend betekent dat het komma van Pythagoras gelijkmatig verdeeld wordt over elk van de 12 halve tonen. In 'welgetemperde' stemmingen als Werckmeister III en Kirnberger worden ze ongelijk verdeeld. Hierbij klinken de centrale toonaarden in de kwintencirkel zo rein mogelijk. De verder verwijderde klinken 'aanvaardbaar'.
De code gekraakt?
Voor Bach wordt hierbij vaak verwezen naarWerckmeister III. Maar in 2005 publiceerde Bradley Lehman een opmerkelijke theorie. Bach zou op de titelpagina van zijn werk zelf aanduidingen getekend hebben over de stemming.

Nu zijn krulletjes niet ongewoon in geschriften van die tijd, maar Lehman plaatste er cijfers bij:
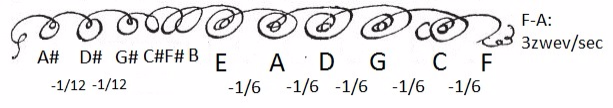
Elk rondje staat voor een opeenvolgende kwint.De C van 'clavier' geeft de C (do) aan. Een extra rondje staat voor een tempering met 1/12e komma van Pythagoras. Twee extra rondjes staat voor een tempering met 2/12e komma of 1/6 komma van Pythagoras.
Als stemhulp zouden de 3 rechtse krulletjes staan voor 3 zwevingen per seconde tussen F en A.
Ter herinnering: 12 kwinten komen net iets hogeruit dan 8 octaven.
De verhouding 12 kwinten/7 octaven = 531441/524288 of 1,0136
Om de kwintencirkel te sluiten, moet dit komma verdeeld worden over een aantal van de 12 halve tonen.
In een kwintencirkel kan je zien hoe de puzzel klopt.

| uitgangspunt | Alle mogelijke toonaarden speelbaar maken. |
| realisatie | Het komma van Pythagoras wordt verdeeld over een aantal kwinten. |
| resultaat | Zelfs voor de verst verwijderde toonaarden klinken zowel kwinten als tertsen erg goed. |