een media hype in 2007
Penrose 1974
Je kunt vlakvullingen maken met vierkanten, gelijkzijdige driehoeken en regelmatige zeshoeken, maar met regelmatige vijfhoekigen, no way!
In 1974 zette Roger Penrose het denken over vlakvullingen op zijn kop. Hij introduceerde een vlakvulling met slechts twee tegels: een vlieger en een pijl, gebaseerd op ... een regelmatige vijfhoek en tienhoek.
Bijzonder aan deze Penrose betegelingen is dat ze aperiodisch zijn, m.a.w. je kan geen willekeurig stuk uit de betegeling zo verschuiven dat het ergens anders past. Er vindt wel lokale 5-voudige symmetrieën, maar het geheel is niet regelmatig. Dit aspect werd opgepikt door o.a. kristallografen en zorgde ook voor mediabelangstelling in 2007 toen het in verband werd gebracht met Islamitische geometrische patronen.
Meer informatie over Penrose betegelingen vind je in een aparte boek.

ophef in 2007
In maart 2007 publiceerden Peter J. Lu (Harvard) en Paul J. Steinhardt (Princeton) een ophefmakend artikel in het tijdschrift Science met als titel “decagonal and Quasicrystalline Tilings in Medieval Islamic Architecture” (Tienvoudige en quasikristallijne betegelingen in middeleeuwse Islamitische architectuur).
Passer en liniaal
De auteurs schrijven dat lange tijd algemeen werd aangenomen dat de decoratieve patronen in de Islamitische bouwkunst steeds werden ontworpen met passer en liniaal. Hieronder zie je hoe je van A tot D met passer en liniaal een regelmatig patroon kunt ontwerpen vanuit een tienpuntige ster.
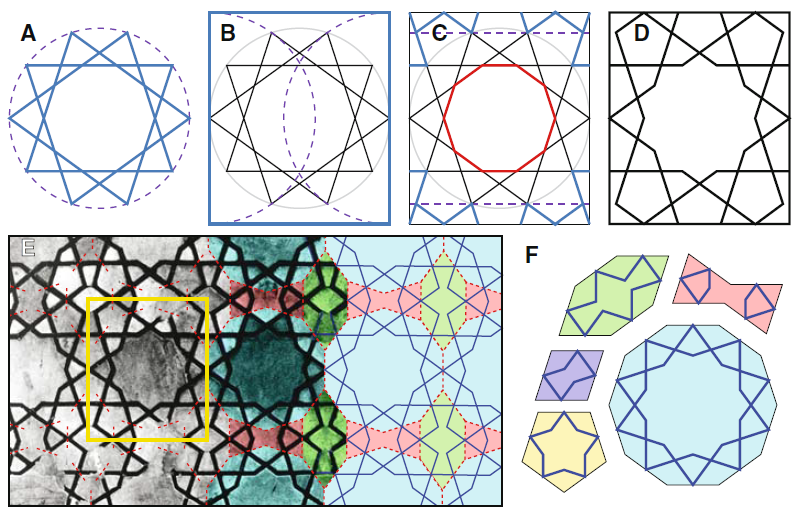
Ze 'suggereren' verder dat rond 1200 nC een nieuwe manier ontstond om dergelijke patronen samen te stellen:
"Rechts in afbeelding E is hetzelfde patroon samengesteld uit een set van veelhoekige gelijkzijdige tegels, met zigzaggende lijnpatronen. Men noemt ze girih tegels, naar het Perzische woord voor 'knoop'. Girih tegels konden gemakkelijk aan elkaar gepast worden en ze gaven de uitvoerders een grote vrijheid om snel complex ogende patronen samen te stellen. In afbeelding F zie je 5 verschillende girih tegels met hun bijkomend patroon van zigzaglijnen."
Opmerking: Kenners van Islamitische kunst kenden al langer het systeem kenden van onderliggende veelhoeken.
Het systeem werd reeds in 1925 gerapporteerd door Ernest Hanbury Hankin, een Brits ambtenaar in India.