Teorema
In ogni triangolo, ciascun lato è minore della somma degli altri due lati.
Ipotesi: ABC è un triangolo
Tesi: BC < AB + AC
Basta dimostrare che quella relazione vale per uno dei lati. Per gli altri si può fare un discorso analogo.
Dimostrazione
Costruzione preliminare
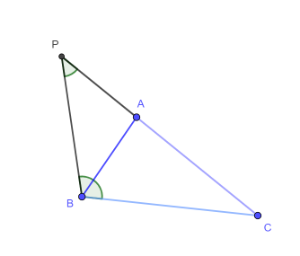
Prolunghiamo il lato AC, dalla parte di A, di un segmento AP AB.
Dato che AP AB, per dimostrare la tesi, basta dimostrare che BC < AP + AC.
Ma AP + AC = PC. Quindi, basta dimostrare che BC < PC.
DIMOSTRAZIONE
Consideriamo il triangolo APB.
Dato che AP AB per costruzione, possiamo dire che il triangolo APB è isoscele e quindi, gli angoli PBA e APB sono congruenti per il teorema del triangolo isoscele.
Consideriamo il triangolo BCP.
L'angolo PBC è maggiore dell'angolo PBA. Pertanto, PBC > PBA BPC.
Quindi, applicando il teorema che dice che se un triangolo ha due angoli non congruenti, allora anche i lati opposti non sono congruenti e in particolare, il lato opposto all'angolo maggiore è maggiore dell'altro, possiamo dedurre che PC > BC che è quello che ci serviva per dimostrare la tesi.