Angoli al centro e angoli alla circonferenza
Angoli corrispondenti
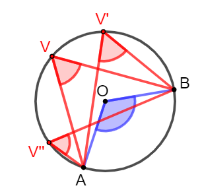
Un angolo al centro e un angolo alla circonferenza si dicono corrispondenti quando insistono sullo stesso arco.
- Per ogni angolo alla circonferenza esiste un unico angolo al centro corrispondente.
- Per ogni angolo al centro, esistono infiniti angoli alla circonferenza corrispondenti.
Teorema: angoli al centro e angoli alla circonferenza
Ogni angolo alla circonferenza è la metà del corrispondente angolo al centro.
La dimostrazione di divide tre parti, trattando i 3 casi:
- O appartiene a uno dei lati dell'angolo alla circonferenza, AVB
- O è interno all'angolo alla circonferenza, AVB
- O è esterno all'angolo alla circonferenza, AVB
1° caso
Ipotesi: AVB è un angolo alla circonferenza e AOB è l'angolo al centro corrispondente
Tesi: AVB AOB
Dimostrazione
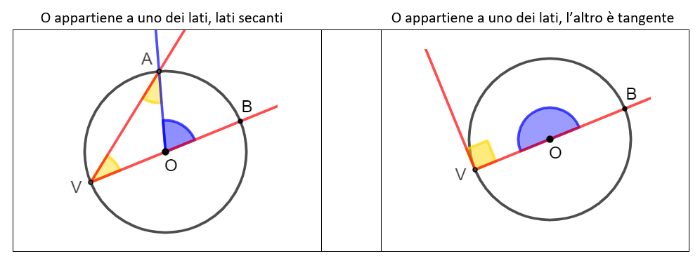
a) O appartiene a uno dei lati dell'angolo AVB; i lati sono entrambi secanti
La tesi è equivalente a AOB 2AVB.
Il triangolo OVA è isoscele, dato che OA e OV sono raggi. Pertanto, gli angoli alla base AVO e OAV sono congruenti.
L'angolo al centro AOB è un angolo esterno del triangolo OVA; quindi, per il teorema dell'angolo esterno,
AOB è uguale alla somma dei due angoli interni non adiacenti, congruenti:
AOB = = + = 2 = 2AVB, da cui =
cioè, l'angolo alla circonferenza è la metà dell'angolo al centro corrispondente.
b) O appartiene a uno dei lati dell'angolo AVB; l'altro lato è tangente alla circonferenza
L'angolo alla circonferenza, che insiste sulla semicirconferenza, è retto, dato che la tangente è perpendicolare al raggio nel punto di tangenza.
L'angolo al centro corrispondente (che insiste sulla semicirconferenza) è piatto.
Pertanto, l'angolo alla circonferenza è la metà dell'angolo al centro corrispondente.
2° caso
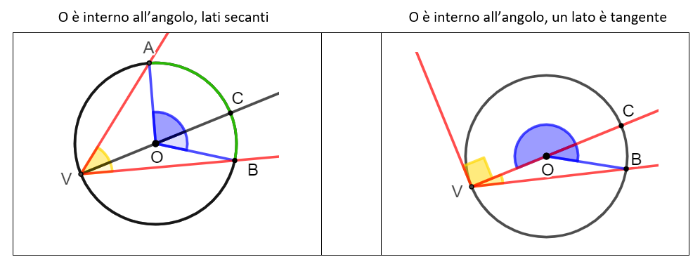
a) O è interno all'angolo AVB; i lati sono entrambi secanti
Tracciando la semiretta VO, l'angolo alla circonferenza AVB viene diviso in due parti che rientrano nel 1° caso della dimostrazione, in quanto i due angoli in cui AVB viene diviso hanno un lato che passa per il centro della circonferenza.
AVB = AVC + CVB e AOB = AOC + COB ;
AOC = 2AVC e COB = 2CVB per la dimostrazione precedente.
Pertanto, possiamo affermare che:
AOB = AOC + COB = 2AVC + 2CVB = 2(AVC + CVB) = 2 AVB
cioè, l'angolo alla circonferenza è la metà dell'angolo al centro corrispondente.
b) O è interno all'angolo AVB; l'altro lato è tangente alla circonferenza
Anche in questo caso, l'angolo alla circonferenza AVB viene diviso in due angoli, di cui uno è retto, che rientrano nel 1° caso della dimostrazione, in quanto i due angoli in cui AVB viene diviso hanno un lato che passa per il centro della circonferenza.
Si ripete il discorso del punto a e si dimostra che l'angolo alla circonferenza è la metà dell'angolo al centro corrispondente.
3° caso
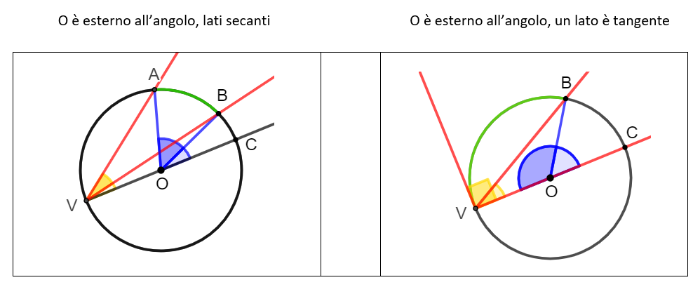
a) O è esterno all'angolo AVB; i lati sono entrambi secanti
Tracciando la semiretta VO, all'angolo alla circonferenza AVB viene accostato un altro angolo BVC. In questo modo si ottengono di nuovo due angoli, AVC e BVC, che rientrano nel 1° caso della dimostrazione, in quanto entrambi hanno un lato che passa per il centro della circonferenza. La differenza rispetto al caso precedente è che AVB non è la somma dei due angoli che hanno un lato passante per il centro della circonferenza, ma la loro differenza.
AVB = AVC - BVC e AOB = AOC - BOC ;
AOC = 2AVC e BOC = 2BVC per la dimostrazione precedente.
Pertanto, possiamo affermare che:
AOB = AOC - BOC = 2AVC - 2BVC = 2(AVC - BVC) = 2 AVB
cioè, l'angolo alla circonferenza è la metà dell'angolo al centro corrispondente.
b) O è esterno all'angolo AVB; l'altro lato è tangente alla circonferenza
Anche in questo caso, l'angolo alla circonferenza AVB è la differenza di due angoli, di cui uno è retto, che rientrano nel 1° caso della dimostrazione, in quanto entrambi hanno un lato che passa per il centro della circonferenza.
Si ripete il discorso del punto a e si dimostra che l'angolo alla circonferenza è la metà dell'angolo al centro corrispondente.