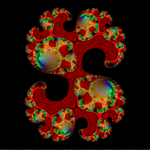
Super zoom Julia
Esta actividad pertenece al libro de GeoGebra Julia y Mandelbrot.
Se recomienda descargar el archivo ggb para una mayor agilidad del escáner.
Hemos visto que, para un determinado valor de la constante c, el conjunto de Julia asociado a c está formado por todos los valores de partida que generan sucesiones acotadas, da igual si son convergentes o caóticas. Pero en vez de limitarse a valores reales (puntos en el eje X) el auténtico conjunto de Julia considera todos los valores complejos (puntos en el plano XY), pues estos "números complejos" también se pueden sumar y multiplicar.
- Nota: aquí consideramos solo los conjuntos de Julia correspondientes a la función f(z) = z2 + c, simbolizados como Jc. Estos conjuntos de Julia se pueden generalizar a otras funciones.
Autor de la actividad y construcción GeoGebra: Rafael Losada.