Transformationen - Strecken und Stauchen
Mithilfe dieses zweiten digitalen Arbeitsblattes sollst du eine weitere Transformation am Graphen untersuchen: das Strecken oder Stauchen von Funktionsgraphen.
Lies dir zunächst folgende Erklärungen durch:
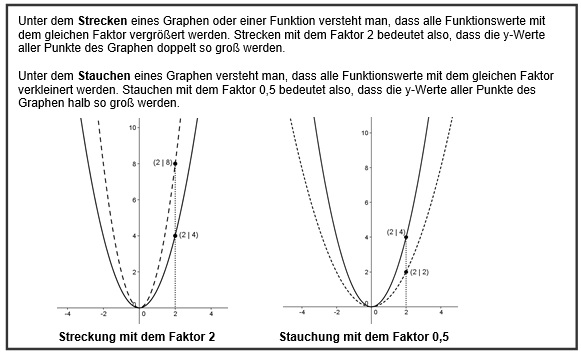
Auch beim Strecken und Stauchen kann man die Richtungen unterscheiden, in welche man den Graphen streckt/staucht.
Beginnen wir mit...
1. Strecken und Stauchen in y-Richtung
Das Strecken und Stauchen in y-Richtung kennst du bereits von Parabeln.
Unten abgebildet siehst du den Graphen der Funktion f(x) = x²-2x+1.
Arbeitsauftrag: Strecke den Graphen der Funktion dem Faktor 2 und anschließend stauche ihn mit dem Faktor 0.5 [in GeoGebra keine Kommas (0,5), sondern Punkte nehmen (0.5)!], indem du die Funktionsvorschrift passend veränderst.
Hinweis: Lege jeweils eine eigene Funktion an. D.h. am Ende sollen 3 Graphen im Fenster zu sehen sein.
Gehe nun genauso bei der folgenden Funktion vor, um diese in y-Richtung zu strecken (Faktor 2) bzw. zu stauchen (Faktor 0.5).
Hinweis: Lege jeweils eine eigene Funktion an. D.h. am Ende sollen 3 Graphen im Fenster zu sehen sein.
Regel: Formuliere nun eine passende Regel: Den Graphen einer Funktion streckt/staucht man mit einem Faktor a in y-Richtung, indem man...
2. Strecken und Stauchen in x-Richtung
Eine Streckung/Stauchung in x-Richtung erreicht man, indem man nicht die gesamte Funktion, sondern nur x selbst multipliziert. Dabei gilt: Wird x mit 2 multipliziert, wird der Graph um den Faktor 1/2 gestreckt. Hier muss man ein bisschen umdenken!
Beispiel:
- Die Funktion f(x) = 2(x-3)²+1 mit dem Faktor 1/2 in x-Richtung gestreckt ergibt die Funktion g(x) = 2(2x-3)²+1.
Du siehst den Graphen der Funktion f(x) = x³- 2x.
Arbeitsauftrag: Strecke und stauche ihn mit den Faktoren 3 und 4 in x-Richtung.
Hinweis: Lege jeweils eine eigene Funktion an. D.h. am Ende sollen 3 Graphen im Fenster zu sehen sein.
Und was passiert bei negativen Streck-/Stauchfaktoren?
Probiere es an den folgenden Funktionen aus und formuliere anschließend deine Beobachtung.
Wie wirken sich negative Streck-/Stauchfaktoren auf den Graphen einer Funktion aus?
Wenn du alle Aufgaben bearbeitet (und ggf. kontrolliert) hast, klicke auf Abgeben! :-)
Hinweis: Wenn noch einiges unklar geblieben ist, findest du im Schulbuch auf Seite 31-33 weitere Erklärungen und Beispiele.
Folgende Fragen sind offen geblieben: