Método de Montecarlo

Tema:Construcciones, Probabilidad, Estadística, Procesos estocásticos o aleatorios

Esta actividad pertenece al libro de GeoGebra Estadística y Probabilidad. La Probabilidad y la Estadística son dos ramas de las Matemáticas que se han desarrollado enormemente en los últimos años, con innumerables aplicaciones en prácticamente todos los campos del conocimiento. Su gran éxito se debe a que permiten prever el comportamiento de un conjunto numeroso de experimentos o individuos. Si lanzamos una moneda al aire no podemos predecir qué lado saldrá, pero si lanzamos muchas monedas (o, equivalentemente, una única moneda muchas veces) podemos prever cuál será su comportamiento de forma aproximada. El método que usaremos se conoce como método de Montecarlo, llamado así en alusión al Casino de Montecarlo (distrito de Mónaco), un centro mundial de los juegos de azar. Porque este método consiste precisamente en hacer un gran número de ensayos "al azar" y simplemente contar cuántos tuvieron éxito. Vamos a ver cómo podemos aprovechar la probabilidad para aproximar el resultado de cálculos complicados sin necesidad de hacerlos. Como queremos comprobar que el método que vamos a seguir funciona, buscaremos un resultado que ya conozcamos de antemano, por ejemplo el valor del número

(aproximadamente 3.1416). Pero no olvides que podríamos hacer lo mismo con valores que no conociéramos: ¡aquí está la fuerza de la probabilidad! Prepararemos el experimento. Observa la siguiente figura. Se trata de una diana circular de radio 1 unidad inscrita en un cuadrado de lado 2 unidades. El área de la diana es

(unidades cuadradas), mientras que el área del cuadrado es de 4 unidades cuadradas.

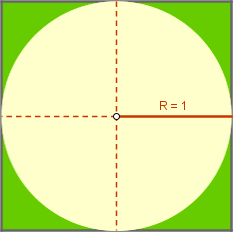Área del círculo:

R² =

1² =

Área del cuadrado: 2 x 2 = 4 Por lo tanto, la fracción de cuadrado ocupada por la diana es

/4.

Ahora efectuamos muchos disparos contra el cuadrado, completamente al azar. Todos darán en el cuadrado, pero no todos darán en la diana. Contamos cuántos dan en cada uno. Si lanzamos muchos, la fracción de disparos que darán en la diana (dianas/disparos) deberá coincidir aproximadamente con la fracción de cuadrado ocupada por la diana, que era la cuarta parte de

. Así que bastará multiplicar por 4 la fracción dianas/disparos para obtener una aproximación de

. Cuantos más disparos realicemos, más probabilidad habrá de que nuestra aproximación de

sea mejor. En la aplicación, usa el botón "Dispara" para realizar disparos de uno en uno, o escribe el número de disparos (no más de 5.000 en cada ocasión) y pulsa el botón "Ráfaga de" para realizar muchos a la vez. Todos los disparos se irán acumulando mientras el ordenador cuenta cuántos han hecho diana (en el modo automático figura el número de dianas en la última ráfaga, mientras que el recuento figuran todas). Por último, el ordenador calcula la fracción dianas/disparos y la multiplica por 4 para obtener una estimación de

1. Realiza varios (más de 20) disparos de uno en uno, pulsando el botón "Dispara" y observa dónde aparecen los impactos. ¿Se distribuyen igualmente separados sobre el cuadrado o de modo desigual?

2. Pulsa el botón "Reinicia". Escribe 5000 (si no está escrito ya) en la casilla de ráfagas y pulsa el botón "Ráfaga de". Realiza la división entre el número de dianas y el número de disparos y multiplica el resultado por 4. ¿Coincide con el valor de estimación de que figura en la aplicación?

3. Sin pulsar el botón "Reinicia", efectúa varias ráfagas de 5000 disparos cada una, anotando en cada caso el número de dianas en cada ráfaga (es el valor que figura en la parte inferior del cuadro "Modo automático"). Después de varias ráfagas, apunta el valor máximo y el valor mínimo de dianas. ¿Te parece que hay mucha diferencia entre ambos valores, comparada con el número de disparos en cada ráfaga? ¿Por qué no se obtienen nunca menos de 3000 dianas, por ejemplo?

4. Después de varias ráfagas de 1000 disparos cada una, hasta superar los 20.000 disparos como mínimo, ¿el valor de que muestra la aplicación comienza por 3.1?

5. No olvides que la aplicación solo cuenta disparos, ¡ella no sabe cuánto vale ! ¿Cómo puede entonces aproximarse al valor real de ? Trata de explicarlo con tus palabras.

Autor de la construcción y la actividad: Rafael Losada Liste. Esta actividad está presente en el Proyecto Gauss

Método de Montecarlo

Nuevos recursos

Descubrir recursos

Descubre temas