Demostraciones de Volumenes
Volumen de Prismas Rectos
El volumen de un prisma recto está dado por el producto del área de su base por su altura, es decir, por la distancia entre las bases. Esto queda expresado en la fórmula:
en que representa el área de la base y representa la longitud de la altura. Esta fórmula es válida para prismas de cualquier base, así como para el cilindro. En el caso de un prisma de base rectangular, cualquier cara puede hacer las veces de base. Su área será el producto de la longitud de dos aristas que convergen en un vértice, y la altura, en tal caso, será la longitud de la tercera arista que converge en ese vértice. De esta forma, el volumen del prisma recto de base rectangular puede expresarse mediante la fórmula: en que a, b y c son las longitudes de las 3 aristas que convergen en uno cualquiera de sus vértices. En el caso particular del cubo, dado que todas sus aristas tienen igual longitud, su volumen queda dado por: en que a es la longitud de su arista.Volumen de una Pirámide
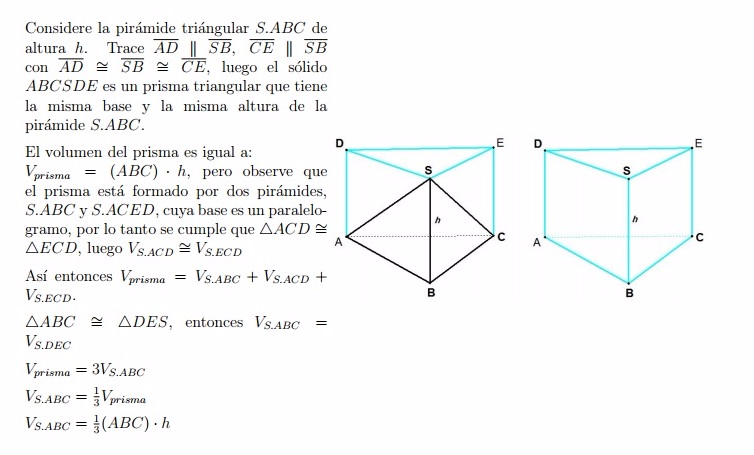
Volumen de un Cono
Dos pirámides de la misma altura y cuyas bases son polígonos equivalentes (de igual área), son equivalentes, o sea tienen el mismo volumen.
Este teorema se puede extender a una pirámide y un cono. Esto es, una pirámide y un cono cuyas bases, polígono y círculo, son equivalentes (tienen igual área), son equivalentes, o sea tienen el mismo volumen.
Lo mismo se podría decir de un cilindro y un prisma.
Por tanto la misma relación que hay entre el volumen de un prisma y el de una pirámide hay entre un cilindro y un cono.
