Posizioni reciproche

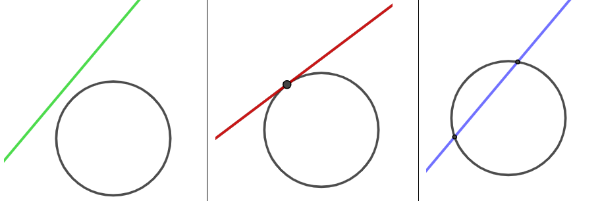
Data una retta e una circonferenza, sono possibili soltanto tre casi:

la retta non ha punti in comune con la circonferenza e si dice esterna
la retta ha un solo punto in comune con la circonferenza e si dice tangente
la retta ha due punti in comune con la circonferenza e si dice secante

Osservazioni

I casi possibili sono solo tre:

nessun punto di intersezione tra retta e circonferenza
un solo punto di intersezione tra retta e circonferenza
due punti di intersezione tra retta e circonferenza

perché per tre punti allineati non passano circonferenze e quindi, una retta e una circonferenza non possono avere tre punti in comune. I punti di intersezione che una circonferenza ha con una retta tangente o con una retta secante sono di tipo diverso tra loro. Come si può vedere traslando la retta nell'immagine che segue, quando una retta secante si sposta "verso l'esterno" della circonferenza, trasformandosi prima in tangente e poi in retta esterna, i due punti di intersezione con la circonferenza si avvicinano sempre di più, fino a coincidere (quando la secante diventa tangente). Quando si descrive questa situazione dal punto di vista algebrico, mettendo a sistema l'equazione della retta con quella della circonferenza per trovare i loro punti di intersezione, si ottiene un'equazione di 2° grado. Il caso della secante si verifica quando il discriminante dell'equazione risolutiva è maggiore di zero e quindi, si hanno due soluzioni reali distinte. Quando invece il discriminante dell'equazione risolutiva è uguale a zero, si ottengono due soluzioni coincidenti e la retta è tangente. Se poi il discriminante dell'equazione risolutiva è minore di zero, non si hanno soluzioni reali e la retta è esterna.

Prova tu: Sposta la retta e osserva i punti di intersezione con la circonferenza

Approfondimento algebrico

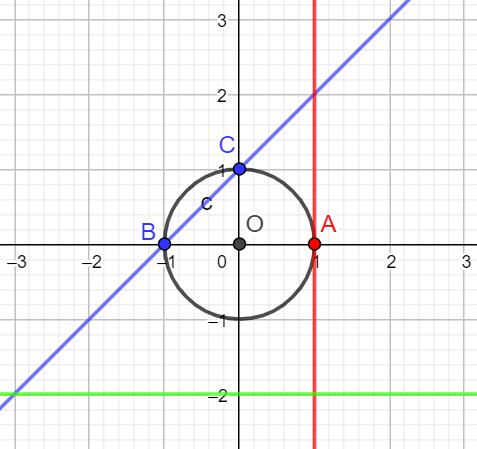
Consideriamo la circonferenza avente il centro nell'origine e raggio 1. La sua equazione è

. Le sue intersezioni con la retta di equazione

si ottengono risolvendo il sistema tra le due equazioni che fornisce l'equazione risolvente

che ha le due soluzioni reali distinte

Sostituendo questi valori, si trova

, rispettivamente. Quindi, le due intersezioni sono i punti

. La retta

è una secante. Le intersezioni con la retta di equazione

si ottengono risolvendo il sistema che fornisce l'equazione risolvente

che ha l'unica soluzione

, contata 2 volte. Pertanto, si ottiene una sola intersezione, il punto

e la retta è tangente. Le sue intersezioni con la retta di equazione

si ottengono risolvendo il sistema che fornisce l'equazione

che non ha soluzioni reali (discriminante negativo); quindi, non ci sono intersezioni e la retta è esterna.

Posizioni reciproche

Osservazioni

Prova tu: Sposta la retta e osserva i punti di intersezione con la circonferenza

Approfondimento algebrico

Nuevos recursos

Descubrir recursos

Descubre temas